Calculations of Radiopharmaceuticals
| Home | | Pharmaceutical Drugs and Dosage | | Pharmaceutical Industrial Management |Chapter: Pharmaceutical Drugs and Dosage: Radiopharmaceuticals
Calculations for radioactive materials are important for dispensing or administering the right dose to a patient has also for the laboratory researcher to use the right amount of the radioactive material.
Calculations
Calculations
for radioactive materials are important for dispensing or administering the
right dose to a patient has also for the laboratory researcher to use the right
amount of the radioactive material. In addi-tion, the phenomenon of radioactive
decay necessitates an understanding of changing radioactivity of a preparation
over a period of time.
Half-life
of a radionuclide is the time taken for half of the radionuclide’s atoms to
decay. Radioactive decay is the process by which an atomic nucleus of an
unstable atom loses energy by emitting ionizing particles. If λ be the rate of decay of a
radionuclide (number of disintegrations per unit time) and τ be the average lifetime of an atom
before it decays, the number N of
radioactive atoms available in a sample at any point in time, t, represented as N(t), is a function of
the number of radioactive atoms present
in the same amount of sample at the initial time point, t = 0, by first-order rate of degradation of the radionuclide
(since the rate of deg-radation depends on the number of available radioactive
nuclei) by the equation:
N(t )
= N ( 0
)e−λt
Note
that this is a typical first-order equation, where a measure of the rate of a
phenomenon [N(t)/N(0)] is an
exponential function of the rate of that phenomenon, λ, times the elapsed time. The minus
in the exponent repre-sents the reduction of radioactivity with time.
Moreover,
since,
λ=1/τ
N(t ) = N ( 0 )e− t/τ
Thus,
radioactive decay is exponential with a constant probability.
Typical
of the first-order reaction kinetics, at half-life, t = t1 2 and
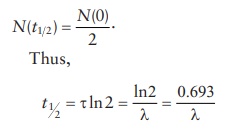
or,
the rate of decay, λ,
can be calculated from t1/2
as:
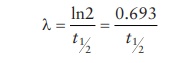
As
seen in this equation, highly radioactive materials (high λ) have a short half-life, whereas
low-radioactivity emitting materials last longer.
Example
Ten
mCi of a radioactive isotope was received in the laboratory on February 15.
This isotope has a half-life of 60 days. How much is the remaining
radioactivity on March 15?
Solution:
Representing
radioactivity as the number of available radionuclides,
N(0) =
10 mCi
t = 30 days
t1/2 = 60 days
N(t)
= ?
Now,
N(t
) = N(0)e−λt
To
use this equation, we need to calculate λ, the rate of decay.
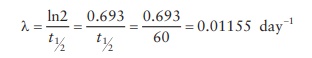
Now,
N(t )
= N(0)e − λt = 10 mCi × e −0.01155 ×30 = 7.07 mCi
Note
that the initial radioactivity of 10 mCi would become 5 mCi in 60 days, since
the t1/2 is 60 days. However,
after 30 days of storage, on day 30, the activity of the radioactive compound
is more than a quarter of the initial radioactivity. This highlights that the
rate of decay of a radioactive compound follows a nonlinear first-order
exponential rate kinetics.
Related Topics
