Hammett Equation

HAMMETT EQUATION

The Hammett equation is a very useful tool for monitoring the extent of charge development in the activated complex. If a substituent is attached to the meta or para position of a benzene ring, it will change the ability of the aromatic ring to donate or withdraw electrons relative to benzene itself. Thus a p-methylphenyl group should be electron donating relative to phenyl while a p-bromophenyl group should be electron withdrawing relative to phenyl. Furthermore, placement of the bromo group in the meta position places it closer to the point of attachment of the phenyl ring so the electron-withdrawing ability of the m-bromophenyl group is greater than that of the p-bromophenyl group. Substituents are normally attached only to the meta or para positions of the phenyl so that they do not sterically interfere with the site of attachment of the phenyl group.

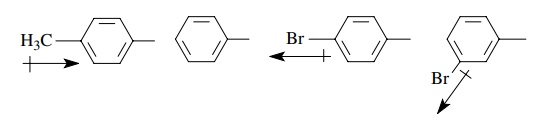
By the use of a model reaction (ionization of benzoic acids), the ability of a substituent to modify the electron-donating or electron-withdrawing ability of the phenyl group and thus influence that reaction can be defined quantitatively by the Hammett equation,

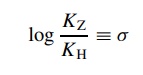
where K_Z is the acidity constant for a benzoic acid with some substituent– Z attached and K_H is the acidity constant for benzoic acid itself.

The result is a substituent constant (σ ) which is a numerical description of the electronic effect of a substituent relative to a hydrogen atom on the model reaction. Stated a different way, a substituent constant σ is a quantitative way to describe the electron-donating or electron-withdrawing properties of a substituent when it is attached to a benzene ring. 

Different σ values are obtained for a given substituent if it is in the meta or the para position so σ values are positionally dependent. Table 5.1 lists some common σ values.

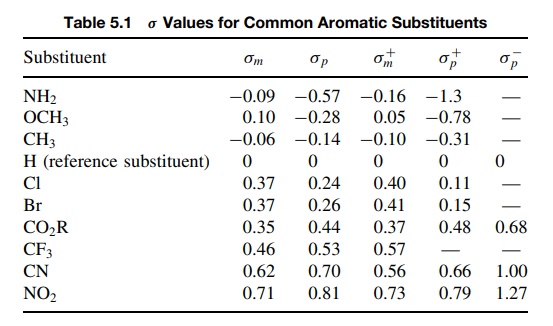
The model reaction used to evaluate σ constants is an ionization equilibrium in which a negative charge is produced upon going from reactants to products. Electron-withdrawing groups have positive σ values because they increase the ionization relative to hydrogen, K_Z/K_H > 1, and log(K_Z/K _H) > 0. Electron-donating substituents have negative σ values because they decrease ionization relative to hydrogen, K_Z/K_H < 1, and log(K_Z/K_H) < 0. Hydrogen itself is treated as a substituent with σ = 0 because K_Z = K_H and thus K_Z/K_H = 1 and log(K_Z/K _H) = 0.

Furthermore the absolute magnitude of the σ value provides a quantitative measure of the relative electron-donating or electron-withdrawing ability. Thus a m-CF₃ group (σ = 0.46) is a stronger electron-withdrawing group than m-Cl (σ = 0.37) but is a less strong electron-withdrawing group than m-CN (σ = 0.62). On the other hand, a p-methyl group (σ = −0.14) is a weaker electron donor than p-OCH₃ (σ = −0.28) but a better electron donor than p-Si(CH₃)₃ (σ = −0.07)

These substituent constants can be used with rate data to evaluate the type and extent of charge development in the activated complex of the rate-determining step for a wide variety of chemical reactions. The rates of reaction for a particular transformation are measured using a series of compounds which differ only by the phenyl substituents present; for example,

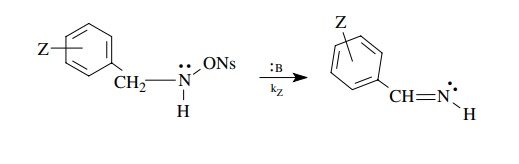
Then the differences in rate caused by the electronic effect of the substituent are correlated by the Hammett equation log(k_z/ k_H) = ρσ_z, where k_z is the rate constant obtained for a compound with a particular meta or para substituent, k_H is the rate constant for the unsubstituted phenyl group, and σ_Z is the sub-stituent constant for each substituent used. The proportionality constant ρ relates the substituent constant (electron donating or withdrawing) and the substituent’s effect on rate. It gives information about the type and extent of charge devel-opment in the activated complex. It is determined by plotting log(k_z/ k_o) versus σ_z for a series of substituents. The slope of the linear plot is ρ and is termed the reaction constant. For example, the reaction shown above is an elimination reaction in which a proton and the nosylate group are eliminated and a C–N π bond is formed in their place. The reaction is second order overall, first order in substrate, and first order in base. The rate constants were measured for several substituted compounds:

These data were plotted according to the Hammett equation to give the plot in Figure 5.17. The first thing to note is that the Hammett plot is linear. The linearity of the plot implies that the substituent constants determined for the ionization of benzoic acids (σ ) are correctly modeling electronic changes taking place in the reaction under consideration; that is, the influence of a substituent on the model reaction is of the same type as for the reaction under investigation.

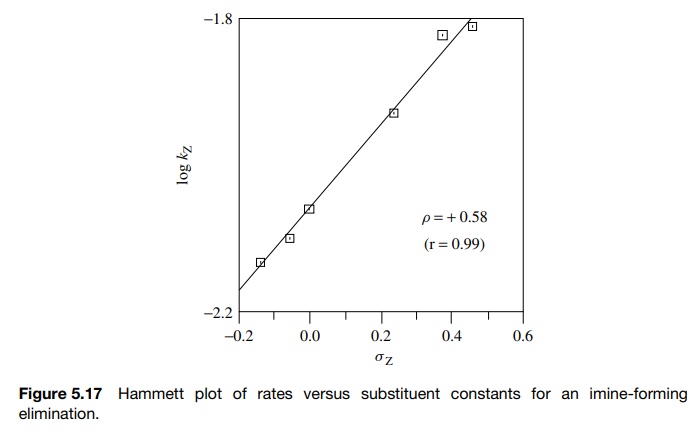
Next the sign and absolute magnitude of the ρ value determined from a Ham-mett plot give information about charge development at the transition state. The sign of ρ tells whether a positive or negative charge is being developed in the activated complex relative to the reactants. A positive ρ value means that elec-tron density is increased (negative charge is being produced) in the activated complex. A negative ρ value means that electron deficiency is being produced (often a positive charge) in the activated complex. Generally ρ values have abso-lute magnitudes between 0 and 3, but values as high as 10 or 12 are known. A value of ρ = 0 means that substituents have no electronic effect on the reaction rate, and thus no charge is being developed at the transition state. Large absolute values of ρ mean that substituents influence the rate greatly, and thus the amount of charge developed in the activated complex is large and influenced significantly by the electronic properties of the substituents. For example,

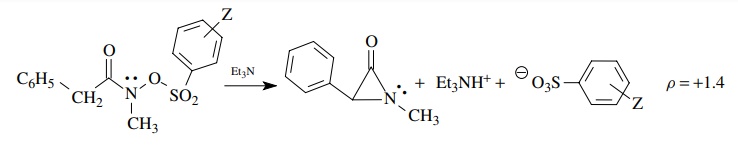
This ρ = 1.4 means that negative charge is being developed on the arenesul-fonate group at the transition state, consistent with this group departing as an anionic leaving group as part of the rate-determining step. The magnitude of 1.4 means that a significant amount of charge is developed on the leaving group. This interpretation is possible only by comparing ρ = +1.4 with ρ values for sulfonate leaving groups in other reactions in which a range of normal values is known. The normal range is about +0.8 to +1.65; therefore the value of 1.4 indicates significant charge development at the transition state. In addition to the positive ρ value, it is also known that the reaction is second order overall, first order in substrate, and first order in triethylamine. 

Moreover, there is a primary kinetic deuterium isotope effect for the benzylic position. These observations allow a detailed structure to be drawn of the activated complex in which concerted 1,3 elimination results in formation of the three-membered ring product.

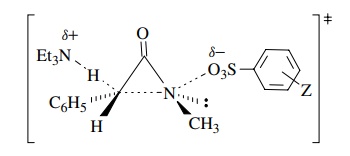
The reaction of N ,N -dimethylbenzylamines with methyl iodide is found to have ρ = −1.0. The negative sign indicates that partial positive charge is being produced in the transition state. The modest size of ρ is consistent with the charge being developed on the nitrogen, which is insulated from the aromatic ring by the saturated CH₂ group. The ability of substituents to influence rate is reduced by the insulating methylene group, and therefore ρ is smaller. In comparison the methylation of N ,N -dimethylaniline has ρ = −3.3 because the nitrogen atom, on which positive charge is developed in the transition state, is directly attached to the phenyl ring and the substituents have a greater influence on the stability of the charge being developed. Hence the magnitude of ρ is much larger.

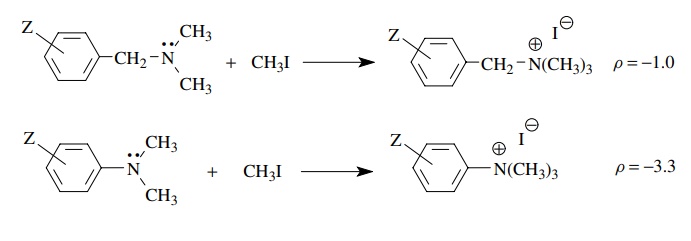
For similar reactions, comparison of the ρ values can be used to determine which reaction has a greater charge development. Comparison of the olefin-forming eliminations below reveals which reaction has greater charge develop-ment at the benzylic position and thus which has a greater degree of proton removal in the activated complex.

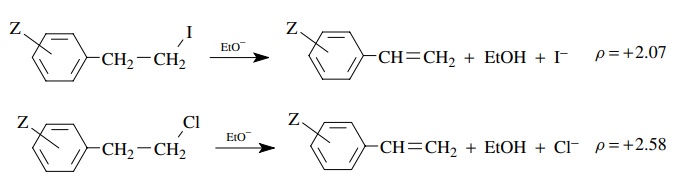
The larger value of ρ = 2.58 for the chloride leaving group than for the iodide leaving group (ρ = 2.07) suggests that greater negative charge is developed on the benzylic position when chloride is the leaving group than when iodide is the leaving group. Base removes the proton to a greater extent for the poorer chloride leaving group than for the better iodo leaving group. Greater electron density on the benzylic position is required to expel the chloride leaving group than the iodide leaving group (i.e., chloride needs a greater “push” than iodide). The transition state for proton removal is later with the chloride leaving group and earlier with the iodide leaving group. These differences in ρ values are thus very useful for discussing changes in the structures of activated complexes and reaction mechanisms caused by structural changes in the reactants.

Sometimes Hammett plots of rates versus σ_z values are nonlinear. When this occurs, it usually indicates that the model reaction from which σ_z values were determined (the ionization of benzoic acids) does not accurately model the elec-tronic changes occurring in the reaction being studied. In most cases this happens when a positive or negative charge is being developed at a position where direct resonance interactions with the substituent magnify the electronic effect of sub-stituents. Usually this happens when charge is developed at a benzylic position or directly on the aromatic ring.

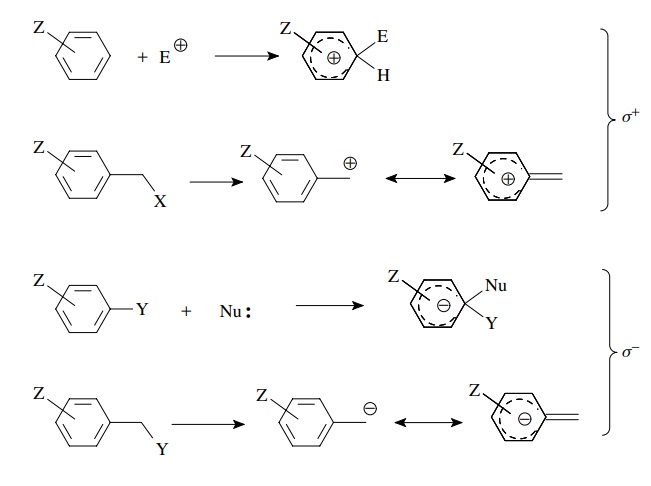
For these cases, new model reactions were developed and the electronic effects of substituents were obtained as σ ⁺ and σ ⁻ substituent constants. The use of σ ⁺ constants is applicable for reactions in which a positive charge is generated on or in direct conjugation with the aromatic ring, while σ ⁻ constants are used for reactions in which a negative charge is generated on or in direct conjugation with the phenyl ring. A listing of these constants is found in Table 5.1. These constants are used in the same way as σ_z constants. Rates are measured and correlated with the appropriate set of σ values (σ, σ ⁺, or σ ⁻) in typical Hammett fashion:

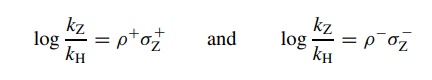
As before, the σ constants are positionally dependent, that is, σ ⁺ meta is different than σ ⁺ para.

A better linear correlation of the rates with a particular set of σ values means that the set of σ values used is a better model for the electronic character of the reaction being studied. Knowing that a better correlation is found for σ ⁺ than σ means that the reaction probably involves positive charge development which can be delocalized directly onto the aromatic ring. 

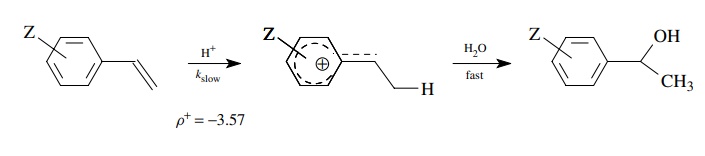
For example, the hydration of substituted styrenes gives a much better linear correlation of log(k_Z/ k_H) versus σ ⁺ than σ . This is consistent with the rate-determining step being protonation of the double bond, giving a benzylic cation. At the transition state, resonance delo-calization of the developing positive charge into the ring accounts for the better correlation with σ_Z⁺ . The value ρ⁺ = −3.57 means that a significant amount of positive charge is developed at the transition state.

The rates of rearrangement of aromatic amine oxides is found to be correlated much better by σ ⁻ than with σ and has ρ⁻ = 3.6. A mechanism consistent with this finding has the oxygen attacking the substituted aromatic ring, thus increasing the electron density on the ring. This charge is delocalized over the aromatic ring by resonance and thus is in direct resonance interaction with substituents in the para position. The process is much better modeled by σ ⁻ than by σ constants.

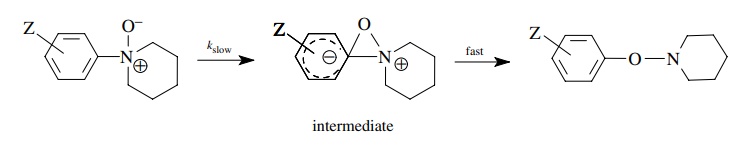
Because of the way in which they were developed, only σ_p⁻ substituent constants are available. If a substituent is meta, then normal σ_m values are used because there is no direct resonance interaction with a substituent in the meta position.

By a variety of techniques, it is possible to gain detailed insight into the structure and properties of the activated complex. This is a remarkable ability considering that the lifetime of the activated complex is on the order of a bond vibration and thus cannot be observed directly. This ability to determine the energy of the transition state and structurally characterize the activated complex is a cornerstone of organic chemistry. It allows us to determine mechanisms of reactions, provides a way to evaluate and predict the effects of structural changes on the reactivity of molecules, and enables us to devise new reactions and processes based on new mechanistic principles that are discovered. The result is an ever-increasing arsenal of reactions than can be used most effectively for carrying out needed organic transformations.