Non-Newtonian flow

Non-Newtonian flow

Most pharmaceutical fluids, such as colloidal dispersions, emulsions, liquid suspensions, and ointments, do not follow Newton’s law of flow. The vis-cosity of the fluid varies with the rate of shear. Depending on how viscosity changes with shear, there are three general types of non-Newtonian flow behaviors: plastic, pseudoplastic, and dilatant (Figure 12.1b–d).

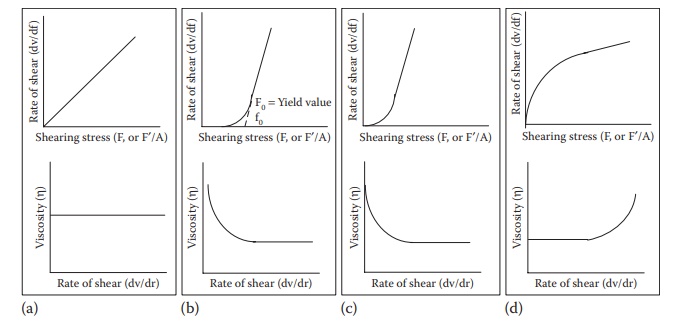
Figure 12.1 Plots of rate of shear and viscosity as a function of shearing stress for (a) Newtonian, (b) plastic, (c) pseudoplastic, and (d) dilatant flows.

Plastic flow

Substances that undergo plastic flow are called Bingham bodies; they are defined as substances that exhibit a yield value as the point at which plas-tic flow curve intersects shearing stress axis (Figure 12.1b). Plastic flow is associated with, for example, the presence of flocculated particles in con-centrated suspensions. Flocculated solids are light, fluffy conglomerates of adjacent particles held together by weak van der Waals forces. A certain shearing stress must be exceeded in order to break up van der Waals forces, which is the yield value, f₀. The yield value is an indicator of flocculation. Higher the yield value, greater the degree of flocculation.

A plastic system resembles a Newtonian system at shear stresses below the yield value. The characteristics of plastic flow can be summarized as follows:

·           Plastic flow does not begin until a shearing stress, corresponding to a yield value, f, is exceeded.

·           The curve intersects the shearing stress axis but does not cross through the origin.

·           The materials are said to be elastic at shear stresses below the yield value.

Pseudoplastic (shear-thinning) flow

Pseudoplastic flow is characterized by decrease in viscosity with increas-ing shear stress. This leads to increasing rate of shear (flow) for the same amount of change in the shear stress as the shear stress levels are increased. Thus, these fluids tend to flow more easily with increasing shear stress and flow and are thus called shear-thinning fluids. The molecular origin of the shear-thinning behavior of fluids is in preferential alignment of the mol-ecules of solution during flow, such that intermolecular cohesion forces are reduced as the rate of shear and the rate of flow increase. Thus, shear thin-ning occurs when molecules align themselves during flow, such that they slip and slide past each other.

Linear polymers in solution exhibit pseudoplastic flow. A large number of pharmaceutical products, including natural and synthetic gums (e.g., liquid dispersions of tragacanth, sodium alginate, methyl cellulose, and sodium carboxymethylcellulose), exhibit pseudoplastic flow properties.

The characteristics of pseudoplastic flow materials can be summarized as follows:

·           Pseudoplastic substances begin to flow when a shearing stress is applied; therefore, they exhibit no, or very low, yield value. Thus, the shear stress—shear rate profile does cross the origin (Figure 12.1c).

·           Viscosity of a pseudoplastic substance decreases with increasing shear stress and shear rate.

Dilatant (shear-thickening) flow

Dilatant flow is characterized by an increase in viscosity with increasing shear stress. This leads to decreasing rate of shear (i.e., reduced flow and higher viscosity) for the same amount of change in the shear stress as the shear stress levels are increased. Thus, these fluids tend to get more viscous and thicker and flow with greater difficulty with increasing shear stress and flow; they are thus called shear-thickening fluids. The molecular origin of the shear-thickening behavior of fluids is in entanglement with increasing attractive intermolecular interactions among the molecules of solution dur-ing flow, such that the intermolecular cohesion forces increase as the rate of shear and the rate of flow increase. Thus, shear thickening occurs when mol-ecules get entangled, swell, or otherwise align themselves during flow, such that the intermolecular forces of attraction are higher as the flow increases.

Generally, dilatant solutions are those that exhibit an increase in solute volume when sheared. This leads to the reduction in free, or unbound, solvent volume between the solute molecules. Thus, the viscosity increases with shear rate. Dilatant systems are usually suspensions with a high per-centage (≥ 50% w/w) of dispersed small, deflocculated particles. These sys-tems exhibit an increase in resistance to flow with increasing rates of shear.

The characteristics of dilatant flow materials can be summarized as follows:

·           Solutes in dilatant solutions increase in volume when sheared. When the stress is removed, the dilatant system returns to its original state of fluidity.

·           Viscosity increases with increasing shear rate.

In concentrated suspensions, particles are closely packed, with the inter-particle void volume being at a minimum at rest. Nevertheless, the amount of vehicle in the suspension is sufficient to fill this volume and to allow the particles to move relative to one another at low rates of shear. Dilatant sus-pensions can be poured from a bottle, since these are reasonably fluid under these conditions. The bulk of the system dilates (expands) with increase in shear stress. The particles in a deflocculated suspension take an open form of packing; that is, each particle is detached from every other particle, occu-pying its own space and interacting with solvent molecules to its full surface. Thus, the solvent-filled interparticle void volume is lower for deflocculated suspensions. Accordingly, resistance to flow increases with an increase in flow, because the particles no longer completely get wetted or lubricated by the vehicle. Eventually, the suspension will set up as a firm paste.

The Newton’s flow equation described earlier, t = η * D, where, D is the rate of flow and t is the applied stress, can be modified to:

 t = η* D*e^N

For Newtonian fluids, N = 0 and the expression e^N = 1, thus yielding the expression for Newtonian flow. For dilatant or shear-thickening fluids, 0 < N < 1. As dilatancy increases, the shear rate response to shear stress decreases exponentially; thus, N decreases as dilatancy increases for shear-thickening fluids.