Reaction Kinetics

REACTION KINETICS

The first step in delineating the mechanism of a reaction is to determine what reactant species must come together to produce the activated complex of the rate-determining step. This can be done by determining the order of the reaction with respect to each of the reactants in the process. If the rate of a reaction is dependent on the concentration of a particular reactant, then that reactant is involved in the transition state of the rate-determining step of that reaction. This provides important structural information about the activated complex since it reveals which chemical species are present in the activated complex.

The order of a reaction is found by determining the relationship between rate and concentration for each reactant. Thus for the elementary process A → B, the rate of reaction ν can be expressed as the decrease in the concentration of reactant A with time or the increase in the concentration of product B with time:

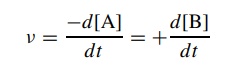
Further, the rate of the reaction can be expressed as a function of the concen-tration of A, where k is the rate constant for the process:

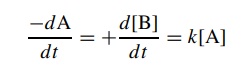
This differential rate expression shows that the reaction rate is directly dependent on the concentration of A — the greater is [A], the faster is A converted to B. The reaction is said to be first order with respect to A because the exponent of [A] is 1.

The above expression is the first-order differential rate law for the conver-sion of A to B. The change in concentration of A over the complete course of the reaction is given by the integrated rate law, which is found by solving the differential rate law:

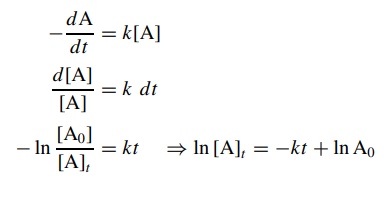
The integrated rate law shows that the natural logarithm of the concentra-tion of the starting material A decreases linearly with time. By determining the concentration of A at various times [A_t ] and plotting ln[A]_t versus t , a straight line with slope −k will be obtained if the reaction is first order in A. (Since the concentration of product at any time [B_t ] = [A₀] − [A_t ], a plot of the increase in the concentration of B with time in the form of ln([A₀] − [B_t ]) versus time would also give a straight line whose slope is +k.) If such linear dependence is observed, then the reaction is first order with respect to A and the rate constant for the reaction can be determined. If the rate plot is not linear, then the reaction is not first order with respect to A; that is, a first-order rate law does not correctly describe the kinetic behavior.

Second-order reactions occur when two reagents must collide in solution to produce the activated complex. Thus for the reactions

2A → B

A+Β → C

each reaction is second order because the sum of the exponents of species in the rate law is 2:

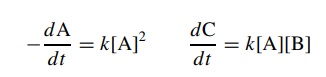
This means that in the first instance two molecules of A must collide to produce the activated complex. In the second case a molecule of A and B collide to produce the activated complex. In each case the second-order dependence requires that both of the colliding molecules are a part of the activated complex of the rate-determining step.

Integration of these differential rate laws gives

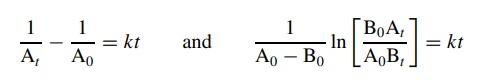
Again plotting concentration versus time using these integrated second-order rate laws gives linear plots only if the reaction is a second-order process. The rate constants can be determined from the slopes. If the concentration – time plots are not linear, then the second-order rate equations do not correctly describe the kinetic behavior. There are integrated rate laws for many different reaction orders.

It is often possible to simplify the rate law of a second-order process by employing pseudo-first-order conditions. For a second-order reaction where

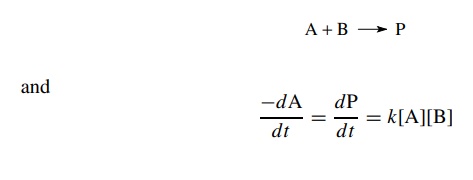
the integrated rate law for a second-order reaction can be used to plot the kinetic data. Alternatively, if the concentration of one of the reactants, for example A, is much larger than the other (10-fold excess minimum, 20-fold better), then its concentration does not change significantly over the course of the reaction; thus [A]_t ≈ [A]₀. The differential rate law can be approximated as

dP/dt = k[A][B] = k[A₀][B] = k’ [B]

where k = k[A]₀. This new rate law is a first-order equation which is much easier to deal with and plot. A plot of ln[B] versus t will give a straight line of slope k’. From k’ and [A]₀ (which is known), the rate constant can easily be determined. This is a much simpler method for determining the rate constant than the normal second-order treatment. The order of the reaction with respect to A can be checked by using several different initial concentrations of [A]₀ and the relationship

 k’= k[A]₀

Therefore

log k’ = log[A]₀ + log k

Plots of log k’ versus log[A]₀ will have unit slope if the reaction is first order in A. Alternatively, doubling [A]₀ should double the rate if the reaction is first order in A.

In a multistep process involving a reactive intermediate, the rate law for the overall reaction cannot be written down a priori because the step in which the reactants disappear is different than the step in which the products are formed (Figure 5.15). In a large number of cases, the intermediate is of high energy and reacts very rapidly — either returning to reactant or going on to product.

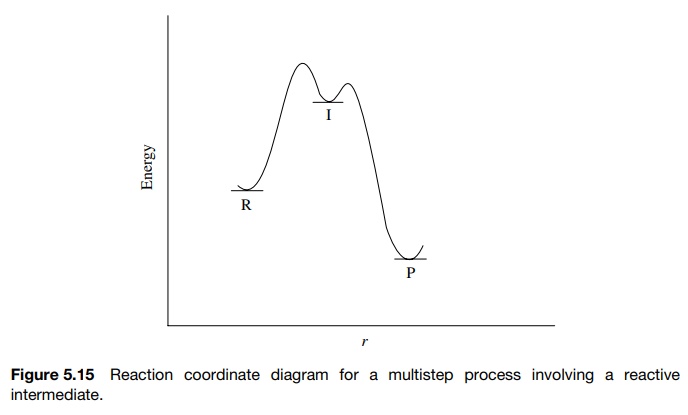
In such cases the steady-state approximation can be used to derive a rate expression that can be tested. Thus for a reaction process involving an intermediate [I]

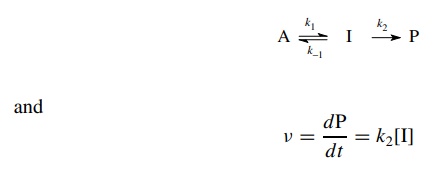
The concentration of the intermediate [I] which gives product is given by the difference between the rate of its formation from A and the rate of its conversion back to reactant A or forward to product P

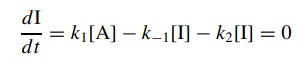
dI/dt = k₁[A] − k₋₁[I] − k₂[I] = 0

The steady-state approximation assumes that since I is very reactive, its concen-tration will be very low at any time during the reaction and it will not change appreciably. Therefore dI/d t = 0. Solving the above expression for the concen-tration of I and substitution into the rate law for the formation product gives

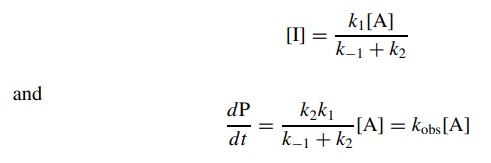
where the observed rate constant k_obs = k₂k₁/ k₋₁ + k₂. This is a first-order rate expression in reactant A and can be integrated and plotted normally.

Several limiting cases can be envisioned for such a multistep process. If k₂ >> k₋₁ (the intermediate goes on to product more rapidly than it returns to reactant),

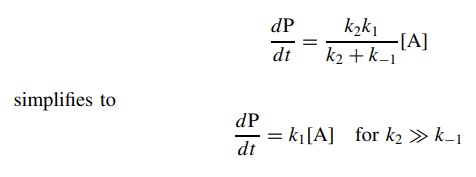
This represents the case where the first step is rate determining. (If this situation is known beforehand, one need not work through the steady-state approximation but merely write down dP/d t = k₁A since the first step is rate limiting and irreversible.)

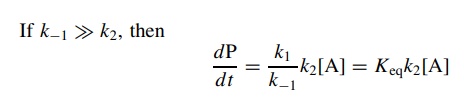
This represents the case where there is a fast preequilibrium preceding the rate-determining step. It is again not necessary to work through the steady-state approximation if this situation is known to exist. If the intermediate I is in equilibrium with the reactant A, then

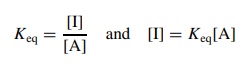
substitution for [I] in the rate expression gives

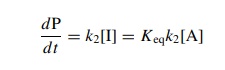
This is actually the correct way to think about this case since the steady-state approximation requires that the concentration of I is low, which it may not be if there is a fast preequilibrium.

If k₂ ≈ k₋₁, then the full steady-state rate expression is needed to describe the rate of reaction:

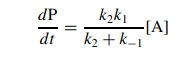
Consider once again the solvolysis of a tertiary bromide in methanol.

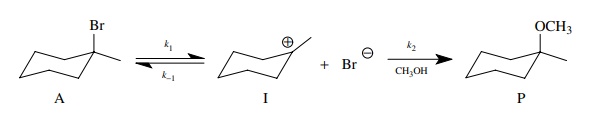
This reaction can be reduced to the kinetic scheme.

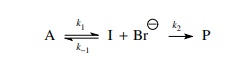
The rate of product formation is given by the pseudo first-order expression in which k₂ = k[CH₃OH] (normally k₂ is taken as the rate constant because the concentration of methanol is constant),

dP/dt = k₂[I]

and the steady-state approximation is written as

dP/dt = O = k₁[A] − k₋₁[I][Br⁻] − k₂[I] d t

Since the return of intermediate I to reactants is a second-order reaction, solving for [I] and substitution into the rate law give

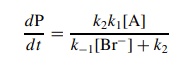
If k₂ >> k₋₁[Br⁻], then ν = k₁[A] and simple first-order behavior is found. If k₋₁[Br] >> k₂, then there is a rapid ionization preequilibrium and

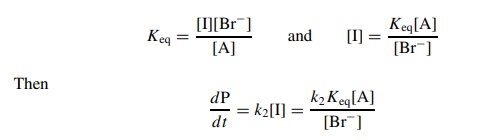
The rate of product formation will be directly proportional to [A] but inversely proportional to [Br⁻]. By using an excess of Br⁻ so that its initial concentration [Br⁻]₀ does not change appreciably over the course of the reaction, pseudo-first-order behavior can be achieved with k_obs = k₂K_eq/[Br⁻]₀.

If k₋₁[Br⁻] ≈ k₂, then the full rate expression will be needed to describe the kinetic behavior. The rate will be first order in [A] and the rate will slow down in the presence of added bromide but not in a simple inverse relationship.