Kinetics of Elimination

KINETICS OF ELIMINATION

The knowledge of kinetics of elimination of a drug provides the basis for, as well as serves to devise rational dosage regimens and to modify them according to individual needs. There are three fundamental pharmacokinetic parameters, viz. bioavailability (F), volume of distribution (V) and clearance (CL) which must be understood. The first two have already been considered.

Drug elimination is the sumtotal of metabolic inactivation and excretion. As depicted in Fig. 2.1, drug is eliminated only from the central compartment (blood) which is in equilibrium with peripheral compartments including the site of action. Depending upon the ability of the body to eliminate a drug, a certain fraction of the central compartment may be considered to be totally ‘cleared’ of that drug in a given period of time to account for elimination over that period.

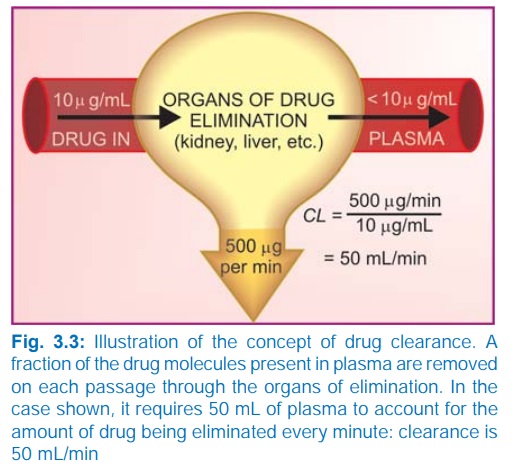
Clearance (CL)

The clearance of a drug is the theoretical volume of plasma from which the drug is completely removed in unit time (analogy creatinine clearance; Fig. 3.3). It can be calculated as

CL = Rate of elimination/C      ...(1)

where C is the plasma concentration.

For majority of drugs the processes involved in elimination are not saturated over the clinically obtained concentrations, they follow:

First order (exponential) kinetics 

The rate of elimination is directly proportional to the drug concentration, CL remains constant; or a constant fraction of the drug present in the body is eliminated in unit time.

Few drugs, however, saturate eliminating mechanisms and are handled by—

Zero order (linear) kinetics The rate of elimination remains constant irrespective of drug concentration, CL decreases with increase in concentration; or a constant amount of the drug is eliminated in unit time, e.g. ethyl alcohol.

The elimination of some drugs approaches saturation over the therapeutic range, kinetics changes from first order to zero order at higher doses. As a result plasma concentration increases disproportionately with increase in dose, (See Fig. 3.5) as occurs in case of phenytoin, tolbutamide, theophylline, warfarin.

Plasma half life 

The Plasma halflife (t½) of a drug is the time taken for its plasma concentration to be reduced to half of its original value.

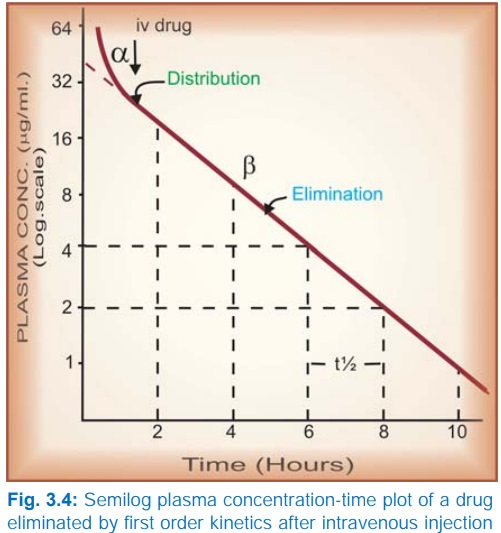
Taking the simplest case of a drug which has rapid one compartment distribution and first order elimination, and is given i.v. a semilog plasma concentrationtime plot as shown in Fig. 3.4 is obtained. The plot has two slopes.

§  initial rapidly declining (α) phase—due to distribution.

§  later less declined (β) phase—due to elimination.

At least two halflives (distribution t½ and elimination t½) can be calculated from the two slopes. The elimination half life derived from the slope is simply called the ‘half life’ of the drug.

Most drugs infact have multicompartment distribution and multiexponential decay of plasma concentrationtime plot. Halflives calculated from the terminal slopes (when plasma concentrations are very low) are exceptionally long, probably due to release of the drug from slow equilibrating tissues, enterohepatic circulation, etc. Only the t½ calculated over the therapeutic plasma concentration range is clinically relevant. It is this t½ which is commonly mentioned.

Mathematically, elimination t½ is

ln2

t½ = ——            ...(2)

k

Where ln2 is the natural logarithm of 2 (or 0.693) and k is the elimination rate constant of the drug, i.e. the fraction of the total amount of drug in the body which is removed per unit time. For example, if 2 g of the drug is present in the body and 0.1 g is eliminated every hour, then k = 0.1/2 = 0.05 or 5% per hour. It is calculated as:

   CL

 k = —–                   ...(3)

        V

V

therefore    t½ = 0.693 × ——     ...(4)

C L

As such, halflife is a derived parameter from two variables V and CL both of which may change independently. It, therefore, is not an exact index of drug elimination. Nevertheless, it is a simple and useful guide to the sojourn of the drug in the body, i.e. after

1 t½ – 50% drug is eliminated.

2 t½ – 75% (50 + 25) drug is eliminated.

3 t½ – 87.5% (50 + 25 + 12.5) drug is eliminated.

4 t½ – 93.75% (50 + 25 + 12.5 + 6.25) drug is eliminated.

Thus, nearly complete drug elimination occurs in 4–5 half lives.

For drugs eliminated by—

First order kinetics—t½ remains constant because V and CL do not change with dose.

Zero order kinetics—t½ increases with dose because CL progressively decreases as dose is increased.

Repeated drug administration

When a drug is repeated at relatively short intervals, it accumulates in the body until elimination balances input and a steady state plasma concentration (Cpss) is attained—

From this equation it is implied that doubling the dose rate would double the average Cpss and so on. Further, if the therapeutic plasma concentration of the drug has been worked out and its CL is known, the dose rate needed to achieve the target Cpss can be determined—

dose rate = target Cpss × CL                 ...(6)

After oral administration, often only a fraction (F) of the dose reaches systemic circulation in the active form. In such a case—

        target Cpss × CL

dose rate = ———————— ...(7)

        F

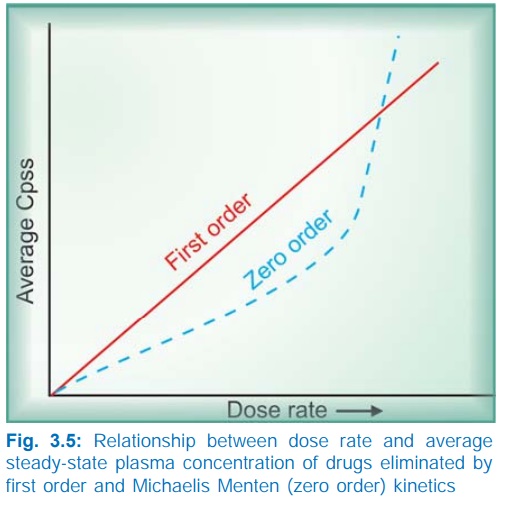
The dose rate Cpss relationship is linear only in case of drugs eliminated by first order kinetics. For drugs (e.g. phenytoin) which follow Michaelis Menten kinetics, elimination changes from first order to zero order kinetics over the therapeutic range. Increase in their dose beyond saturation levels causes an increase in Cpss which is out of proportion to the change in dose rate (Fig. 3.5). In their case:

          (V_max) (C)

Rate of drug elimination = ————— ...(8)

                                                K_m + C

where C is the plasma concentration of the drug, V_max is the maximum rate of drug elimination, and K_m is the plasma concentration at which elimination rate is half maximal.

Plateau Principle

When constant dose of a drug is repeated before the expiry of 4 t½, it would achieve higher peak concentration, because some remnant of the previous dose will be present in the body. This continues with every dose until progressively increasing rate of elimination (which increases with increase in concentration) balances the amount administered over the dose interval. Subsequently plasma concentration plateaus and fluctuates about an average steadystate level. This is known as the plateau principle of drug accumulation. Steadystate is reached in 4–5 half lives unless dose interval is very much longer than t½ (Fig. 3.6).

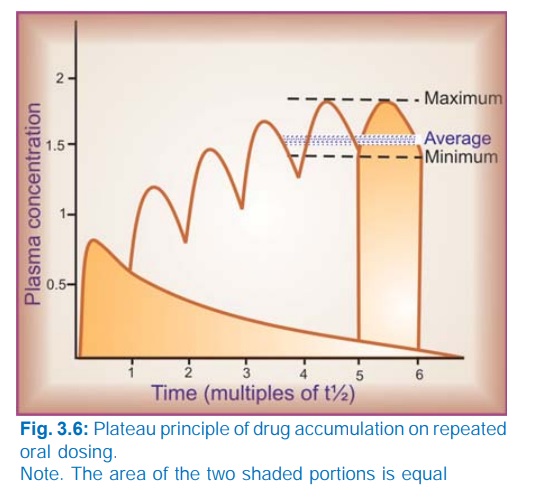
The amplitude of fluctuations in plasma concentration at steadystate depends on the dose interval relative to the t½, i.e. the difference between the maximum and minimum levels is less if smaller doses are repeated more frequently (dose rate remaining constant). Dose intervals are generally a compromise between what amplitude of fluctuations is clinically tolerated (loss of efficacy at troughs and side effects at peaks) and what frequency of dosing is convenient. However, if the dose rate is changed, a new average Cpss is attained over the next 4–5 half lives. When the drug is administered orally (absorption takes some time), average Cpss is approximately 1/3 of the way between the minimal and maximal levels in a dose interval.

Target Level Strategy

For drugs whose effects are not easily quantifiable and safety margin is not big, e.g. anticonvulsants, antidepressants, lithium, antiarrhythmics, theophylline, some antimicrobials, etc. or those given to prevent an event, it is best to aim at achieving a certain plasma concentration which has been defined to be in the therapeutic range; such data are now available for most drugs of this type.

Drugs with short t½ (upto 2–3 hr) administered at conventional intervals (6–12 hr) achieve the target levels only intermittently and fluctuations in plasma concentration are marked. In case of many drugs (penicillin, ampicillin, chloramphenicol, erythromycin, propranolol) this however is therapeutically acceptable.

For drugs with longer t½ a dose that is sufficient to attain the target concentration after single administration, if repeated will accumulate according to plateau principle and produce toxicity later on. On the other hand, if the dosing is such as to attain target level at steady state, the therapeutic effect will be delayed by about 4 half lives (this may be clinically unacceptable). Such drugs are often administered by initial loading and subsequent maintenance doses.

Loading Dose

This is a single or few quickly repeated doses given in the beginning to attain target concentration rapidly. It may be calculated as—

                              target Cp × V

Loading dose = ——————       ...(9)

      F

Thus, loading dose is governed only by V and not by CL or t½.

Maintenance Dose

This dose is one that is to be repeated at specified intervals after the attainment of target Cpss so as to maintain the same by balancing elimination. The maintenance dose rate is computed by equation (7) and is governed by CL (or t½) of the drug. If facilities for measurement of drug concentration are available, attainment of target level in a patient can be verified subsequently and dose rate adjusted if required.

Such two phase dosing provides rapid therapeutic effect with long term safety; frequently applied to digoxin, chloroquine, long acting sulfonamides, doxycycline, amiodarone, etc. However, if there is no urgency, maintenance doses can be given from the beginning. The concept of loading and maintenance dose is valid also for short t½ drugs and i.v. administration in critically ill patients, e.g. lidocaine (t½ 1.5 hr) used for cardiac arrhythmias is given as an i.v. bolus dose followed by slow i.v. infusion or intermittent fractional dosing.

Monitoring Of Plasma Concentration Of Drugs

It is clear from the above considerations that the Cpss of a drug attained in a given patient depends on its F, V and CL in that patient. Because each of these parameters varies considerably among individuals, the actual Cpss in a patient may be 1/3 to 3 times that calculated on the basis of population data. Measurement of plasma drug concentration can give an estimate of the pharmacokinetic variables in that patient and the magnitude of deviation from the ‘average patient’, so that appropriate adjustments in the dosage regimen can be made.

In case of drugs obeying first order kinetics:

Therapeutic drug monitoring (TDM) is particularly useful in the following situations:

Drugs with low safety margin—digoxin, anticonvulsants, antiarrhythmics, theophylline, aminoglycoside antibiotics, lithium, tricyclic antidepressants.

If individual variations are large—antidepressants, lithium.

Potentially toxic drugs used in the presence of renal failure—aminoglycoside antibiotics, vancomycin.

In case of poisoning.

In case of failure of response without any apparent reason—antimicrobials.

To check patient compliance—psychopharmacological agents.

Selection of the correct interval between drug administration and drawing of blood sample for TDM is critical, and depends on the purpose of TDM as well as the nature of the drug.

a. When the purpose is dose adjustment: In case of drugs which need to act continuously (relatively longacting drugs), it is prudent to measure the trough steadystate blood levels, i.e. just prior to the next dose, because this is governed by both V and CL. On the other hand, for shortacting drugs which achieve therapeutic levels only intermittently (e.g. ampicillin, gentamicin), sampling is done in the immediate postabsorptive phase (usually after 1–2 hours of oral/ i.m. dosing) to reflect the peak levels.

          In case of poisoning: Blood for drug level estimation should be taken at the earliest and then repeatedly to confirm the poisoning and to monitor the progress.

          For checking compliance to medication: Even random blood sampling can be informative.

Monitoring Of Plasma Concentration Is Of No Value For

§  Drugs whose response is easily measurable— antihypertensives, hypoglycaemics, diuretics, oral anticoagulants, general anaesthetics.

§  Drugs activated in the body—levodopa.

§  ‘Hit and run drugs’ (whose effect lasts much longer than the drug itself)—reserpine, guanethidine, MAO inhibitors, omeprazole.

§  Drugs with irreversible action—organophosphate anticholinesterases, phenoxybenzamine.