Hygrometry, the Measurement of Humidity

HYGROMETRY, THE MEASUREMENT OF HUMIDITY

The accurate determination of the humidity of air is carried out gravimetrically. The water vapor present in a known volume of air is chemically absorbed with a suitable reagent and weighed. In other less laborious methods, the humidity is derived from the dew point or the wet bulb depression of a water vapor–air mixture.

The dew point is the temperature at which a vapor-gas mixture becomes saturated when cooled at constant pressure. If air of the condition denoted by point A in Figure 6.1 is cooled, the relative humidity increases until the mixture is fully saturated. This condition is given by point B at which the temperature coordinate is the dew point. This can be measured rapidly by evaporating ether in a silvered bulb. The temperature at which dew deposits from the surrounding air is noted, and the humidity is read directly from a psychrometric chart.

The derivation of the humidity from the wet bulb depression requires a preliminary study of the transfer of mass and heat at a boundary between air and water. Since this process is also of importance in the study of drying, a detailed explanation is set out below. If a small quantity of water evaporates into a large volume of air, conditions that make the change in humidity negligible, the latent heat of evaporation is supplied from the sensible heat of the water. The latter cools, and the temperature gradient between water and air promotes the flow of heat from the surrounding air to the surface. As the temperature falls, the rate of heat flow increases until it equals the rate at which heat is required for evaporation. The temperature at the surface then remains constant at what is known as the wet bulb temperature. The difference between the air temperature and the wet bulb temperature is the wet bulb depression. If these temperatures are denoted by T_a and T_wb, the rate of heat transfer, Q, is given by equation (6.1).

Q = hA(T_a - T_wb)                                (6:1)

where A is the area over which heat is transferred and h is the heat transfer coefficient. Mass transfer of water vapor from the water surface to the air is described by equation (6.2).

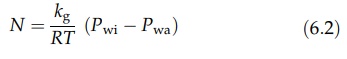
where P_wi is the partial pressure of water vapor at the surface and P_wa is the partial pressure of water vapor in the air. kg is a mass transfer coefficient, and N is the number of moles transferred from unit area in unit time. Rewriting this equation in terms of the mass, W, transferred at the whole surface in unit time, where Mw is the molecular weight of water vapor and A is the area of the surface:

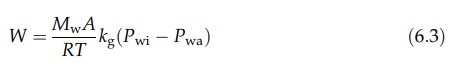
If the partial pressure of water vapor in a system has the value P_w, then, from the general gas equation, the mass of vapor in unit volume is P_wM_w/RT. Sim-ilarly, if the total pressure is P, the mass of air in unit volume is (P–P_w)M_a/RT, where M_a is the “molecular weight” of the air. The humidity, H, is the ratio of these two quantities:

If P is very much greater than P_w, H = P_wM_w/PM_a. Rearrangement and the substitution of humidity for partial pressure in equation (6.3) give

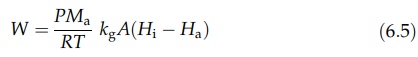
where H_a is the humidity of the air and H_i is the humidity at the surface. The latter is known from the vapor pressure of water at the wet bulb temperature. Since PM_a/RT = ρ, equation (6.5) can be written as

W = ρk_gA(H_i - H_a)                    (6:6)

where ρ is the density of the air. If the latent heat of evaporation is λ, the heat transfer rate necessary to promote this evaporation is given by

Q = ρk_gA(H_i - H_a)                  (6:7)

Equating the expressions (6.7) and (6.4) then gives

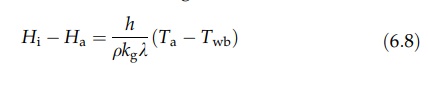
Both the heat and mass transfer coefficients are functions of air velocity.

However, at air speeds greater than about 4.5 m/sec, the ratio h/k_g is approx-imately constant. The wet bulb depression is directly proportional to the difference between the humidity at the surface and the humidity in the bulk of the air.

In the wet and dry bulb hygrometer, the wet bulb depression is measured by two thermometers, one of which is fitted with a fabric sleeve wetted with water. These are mounted side by side and shielded from radiation, an effect neglected in the derivation above. Air is then drawn over the thermometers by means of a small fan. The derivation of the humidity from the wet bulb depression and a psychrometric chart will be discussed later.

Many wet and dry bulb hygrometers operate without any form of induced air velocity at the wet bulb. This may be explained by examining another air-water system. If a limited quantity of air and water is allowed to equilibrate in conditions in which heat is neither gained nor lost by the system, the air becomes saturated and the latent heat required for evaporation is drawn from both fluids, which will cool to the same temperature. This temperature is the adiabatic saturation temperature, T_s. It is a peculiarity of the air-water system that the adiabatic saturation temperature and the wet bulb temperature are the same. If water at this temperature is recycled in a system through which air is passing, the incoming air will be cooled until it reaches the adiabatic saturation temperature at which point it will be saturated. The temperature of the water, on the other hand, will remain constant, and all the latent heat required for evaporation will be drawn from the sensible heat of the air. Equilibrium is then expressed by the following equation:

(T_a - T_∞)S = (H_∞ - H_a) λ                     (6:9)

where T_a is the temperature of the incoming air and S is its specific heat. H_a and H_∞ are the humidities of the incoming air and the saturated air, and λ is the latent heat of evaporation for water.

The process of adiabatic saturation in which the humidity progressively rises and the temperature progressively falls is described on a humidity chart by adiabatic cooling lines, which run diagonally to the saturation curve. Charts are specially constructed so that these lines become parallel.

If a wet and dry bulb hygrometer is exposed to still air, the region adjacent to the wet bulb closely resembles the system described above. After a consid-erable period, equilibrium will be attained and the wet bulb will record the adiabatic saturation temperature.

When both wet and dry bulb temperatures have been found, the humidity is read from the psychrometric chart in the following way. The point on the saturation curve corresponding to the wet bulb temperature is first found. An adiabatic cooling line is then interpolated and followed until the coordinate corresponding to the dry bulb temperature is reached. The humidity is read from the other axis.

The change in the physical properties of a hair or fiber with change in humidity is utilized in many instruments. After calibration, they are suitable for use over a limited range of humidity.