Cell Kinetics

CELL KINETICS

Definitions

The principles of bioreactor design require understanding the phenomena intended to take place in these controlled environments. This relates to the growth kinetics of prokaryotic or eukaryotic cells derived from animal, plant, or microbial origins. The complexity of biochemical reactions and transport phe-nomena render accurate predictive mathematical modeling impossible since the system consists of multiple phases having many components. Attempts have been made to estimate growth kinetics based on a matrix combining unstruc-tured or structured approaches to distributed or segregated models (Table 16.2).

Growth Cycle

The growth cycle of cells has been documented for over a century. It consists of six phases that describe cells growth from an initial period of accommodation or acclimatization through to exhaustion or overpopulation of the environment. The lag phase, which occurs when cells are introduced into a medium, is a period of time when no net change in cell number occurs. This phase is followed by an accelerated growth phase when the cell numbers start to increase and the division rate increases to reach a maximum in the exponential growth phase, where the division rate is proportional to dln C_n0/dt, which is constant at maximum value. Following this maximal growth rate, a deceleration in both growth and division occurs. The cell population finally reaches a maximum value, but the death of growing cells occurs as nutrients are depleted.

TABLE 16.2 Various Models for Cell Kinetics

Monod Kinetic Parameters

Much has been written regarding the growth of cells in fermenters and chemostats (Lee, 1992). The kinetic considerations in these systems are briefly summarized below.

The Monod equation is an empirical expression describing the effect of substrate concentration on the specific growth rate, and it takes a form similar to Michaelis–Menton enzyme kinetics or the Langmuir adsorption isotherm:

where μ and μ _max are growth rate and specific growth rate at half-maximum value, and K_s and C_s are a system coefficient and concentration of the limiting substrate in the medium, respectively.

Monod kinetic parameters specific growth rate at half-maximum and the system coefficient cannot be estimated with a series of individual studies as easily as Michaelis–Menton kinetics for enzyme action. The initial reaction rate can be measured accurately as a function of substrate concentration for enzymes. Cell cultures undergo an initial lag phase in growth in which Monod kinetics do not apply. Even though the Monod equation has the same form as the Michaelis–Menton equation, the rate equation is different.

The Michaelis–Menton equation describing enzyme activity takes the form

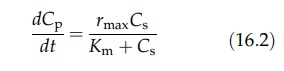
where C_p and C_s are product concentration and substrate concentration, respectively, and K_m is the rate constant. The Monod equation takes the form

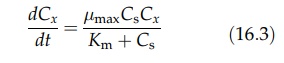
Note that the cell concentration term C_x in the Monod equation is absent from the Michaelis–Menton equation.

Measuring the steady-state substrate concentration at various flow rates, one can test various kinetic models and estimate the value of the kinetic parameters.

A linear relationship can be derived as follows:

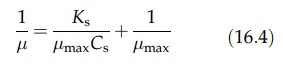
where μ is equal to the dilution rate (D) for a chemostat. If a certain microorganism follows Monod kinetics, the plot of 1/ μ versus l/C_s yields the values of μ _max and K_s by reading the intercept and the slope of the straight line. This plot is the same as the Lineweaver–Burk plot for Michaelis–Menton kinetics. Since 1/ μ approaches infinity as the substrate concentration decreases, the data is weighted too heavily at low substrate concentrations and insuffi-ciently at high substrate concentrations. Nevertheless, this approach has the advantage of showing the relationship between the independent (C_s) and dependent variables (μ). Figure 16.1 illustrates the manner in which the specific growth rate may be derived from a plot of reciprocal dilution rate versus reciprocal substrate rate.

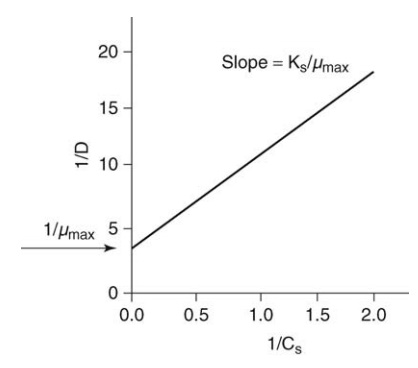
FIGURE 16.1 Reciprocal dilution rate for a chemostat plotted against reciprocal substrate concentration.