Nuclear Magnetic Resonance

NUCLEAR MAGNETIC RESONANCE

The speed with which NMR spectroscopy has been incorporated into scientific inquiry is truly amazing. The first commercial spectrometers became available in the 1950s. By the middle 1980s whole bodies could be placed in the probes of NMR spectrometers (magnetic resonance imaging) and the structures of body parts could be determined in exquisite detail. Today structures of proteins and other macromolecules in solution or in the solid state are determined routinely. What was unthinkable in the 1960s is routinely practiced today even by under-graduates! The power of the method and the structural detail it provides have no doubt fueled its rapid development.

Nuclear magnetic resonance spectroscopy is possible due to the absorption of energy at particular frequencies by atomic nuclei when they are placed in a magnetic field. Most atomic nuclei are characterized by a property termed spin, and this gives rise to a magnetic moment associated with that nucleus. The magnitude of the magnetic moment of the nucleus, which is also quantized by the spin quantum number, is characteristic of that nucleus. Nuclei such as ¹²C, ¹⁶O, and ³²S have nuclear magnetic moments of zero. Other nuclei such as ¹H, ¹¹B, ¹³C, ¹⁵N, ¹⁷O, ¹⁷O, ¹⁹F, and ³¹P have finite magnetic moments and spin quantum numbers of I = 1/2 and are most useful in NMR measurements. Still other nuclei such as ²D and ¹⁴N have finite magnetic moments but spin numbers I > 1/2 and are much more difficult to deal with, although today’s NMR instruments handle these elements routinely as well.

Fortunately for organic chemists, hydrogen and carbon are the most common nuclei found in organic compounds, and the ability to probe these nuclei by NMR is invaluable for organic structure determination. Since proton magnetic resonance (PMR) is the most common type, the behavior of ¹H nuclei in magnetic fields will serve as a model for other nuclei which have spin quantum numbers I = 1/2 and thus behave similarly (¹³C, ¹⁹F, etc.).

The proton has a nuclear magnetic moment (denoted as a vector quantity) which under normal circumstances can adopt any spatial orientation. Since this magnetic moment is a nuclear property, each hydrogen in a molecule has an identical nuclear magnetic moment. When placed in a strong magnetic field, the magnetic moment of the nucleus interacts with the magnetic field. The strength of the interaction depends on the strength of the applied field (H₀) and the nuclear magnetic moment characterized by the magnetogyric ratio γ (the same for all hydrogens but different for other nuclei).

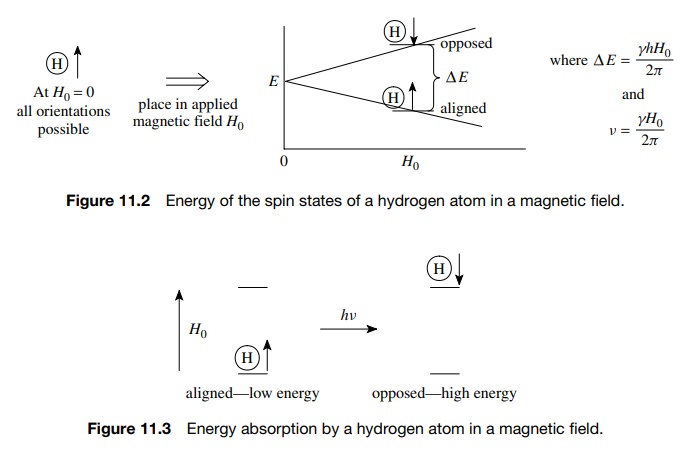
In a strong magnetic field the nuclear magnetic moment is no longer free to adopt just any orientation. Instead the spin quantum number of I = ¹₂ for the hydrogen nucleus results in only two allowed orientations (2I + 1) of the nuclear moment relative to the direction of the applied field — either aligned with H₀ (lower energy) or opposed to it (higher energy.) The difference in energy (ΔE) between the two states is given by ΔE = γ hH₀/2π and is dependent on the cross product of the strength of the applied field H₀ and the magnetic moment of the hydrogen (γ ). Since γ is the same for all hydrogen nuclei, the energy difference between the two allowed orientations is proportional only to the strength of the applied field (Figure 11.2).

If the magnetic field H₀ is fixed and held very constant, then the energy gap between the two spin states of the hydrogen nuclei will remain constant.

Irradiation of the system with radiation of the appropriate frequency ( ΔE= hν) will cause the energy to be adsorbed and the spin of the nucleus will flip from the low-energy state (aligned) to the higher energy state (opposed). It is this absorption of energy which is used to probe the structural features of the molecule (Figure 11.3).

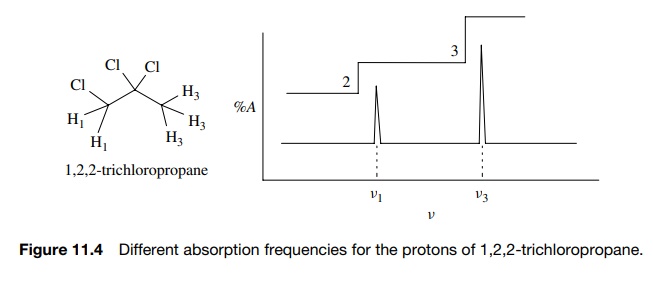
Now since the magnetic moment of a nucleus (γ ) is an atomic property, for a given magnetic field H₀, all hydrogens should absorb energy at the same frequency. However, examination of a molecule such as 1,2,2-trichloropropane (see Fig. 11.4) reveals that the two different types of hydrogens (H₁ and H₃) absorb at two different frequencies (ν₁ and ν₃) (Figure 11.4).

Since the applied field H₀ is constant and all hydrogen nuclei have the same magnetic moment γ , the fact that H₁ and H₃ absorb at two different frequencies requires that the magnetic field that is actually experienced by each set of nuclei (H_eff) is different. Stated differently, even though a constant magnetic field H₀ is applied to the sample, each type of hydrogen H₁ and H₃ experiences a unique magnetic field H_eff (where H_eff ≠ H₀) and consequently absorbs energy at a unique frequency ν₁ and ν₃. Thus the different types of protons are distinguished by different frequencies at which they absorb energy. Furthermore, integration of the absorption intensities of the two signals gives a 3 : 2 ratio which corresponds to the smallest whole-number ratio of each type of proton present. (The integrated area of the peak is given by the step height on the integration curve.) Thus ¹H NMR is able to distinguish different types of protons in a molecule and tell how many there are (at least by ratio).