Newtonian flow

Newtonian flow

Newton’s law of flow states that the application of stress on a liquid leads to flow in the direct proportion to the amount of stress applied. The constant that relates the flow of a liquid to the applied stress is called viscosity, η. Thus,

 t = η•D

where, D is the rate of flow and t is the applied stress.

Fluids that obey Newton’s law of flow are referred to as Newtonian fluids, and fluids that deviate from the linear stress–flow proportionality expressed by the Newton’s law are called non-Newtonian fluids.

Viscosity can also be expressed as the constant that relates the shearing stress (force per unit area applied parallel to the direction of flow of liquid) and shear rate (volume of fluid flow per unit area of the liquid). Thus,

where:

force per unit area (F′/A) required to bring about flow is called the shearing stress (F)

 dv/dr is the rate of shear representing the velocity of fluid movement per unit distance from the plane of shear stress

The units of F′/A are dynes per cm² or Pzascal. The units of dv/dr are (cm/sec)/cm = sec⁻¹. Thus, the Standard International (SI) unit of viscos-ity is Pascal*second (Pa*s). The more commonly used unit of viscosity is dyne*second/cm², which is named Poise (P).

10 Poise = 1 Pascal*second

10 centiPoise = 1 Poise

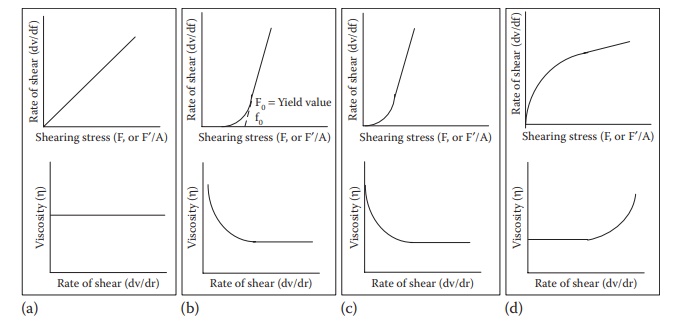
Figure 12.1 Plots of rate of shear and viscosity as a function of shearing stress for (a) Newtonian, (b) plastic, (c) pseudoplastic, and (d) dilatant flows.

The higher the viscosity of a liquid, the greater the shearing stress required to produce a certain rate of shear. A plot of the rate of shear against shearing stress yields a rheogram. A Newtonian fluid will plot a straight line, with the slope of the line being η (Figure 12.1a).

Another term, fluidity, ϕ, is defined as the reciprocal of viscosity:

 Φ = 1/η                    (12.2)

In the case of Newtonian fluids, viscosity is a constant for a fluid at a given temperature and pressure. It does not change with increasing shear rate. Water and dilute solutions typically exhibit Newtonian flow properties.

Temperature dependence and viscosity of liquids

Viscosity of a liquid generally decreases as the temperature is raised. Increased Brownian motion, rapid movement of liquid molecules among each other, at higher temperatures reduces energy expense from the shear-ing force in overcoming intermolecular cohesion forces, leading to a greater proportion of energy utilized in influencing the direction of flow. In other words, fluidity increases with an increase in temperature.

The relationship between viscosity and temperature can be represented by the following equation, which is analogous to the Arrhenius equation of chemical kinetics:

η = Ae^{Ev /RT}                (12.3)

where:

η is the viscosity (centiPoise)

A is the constant, depending on molecular weight and molar volume of liquid

E_v is the activation energy required to initiate flow between molecules (cal/mol)

R is the gas constant (1.987 cal*K⁻¹*mol⁻¹)

T is the temperature in Kelvin

This equation predicts that the decrease in viscosity with an increase in temperature is nonlinear and follows an exponential profile. Thus, from the temperature of highest viscosity of the fluid, slight changes in tempera-ture lead to much more change in fluid viscosity compared with the effect of temperature on viscosity close to the lowest viscosity of a fluid. The temperature–viscosity relationships are critical for routine handling of liquids in pharmaceutical manufacturing under ambient temperature conditions and handling of drug products by patients. For example, an injectable solution stored in a refrigerator may have much higher viscosity and may be difficult to inject than the same solution brought to room temperature before injection.