Alkali metal ions

Alkali metal ions

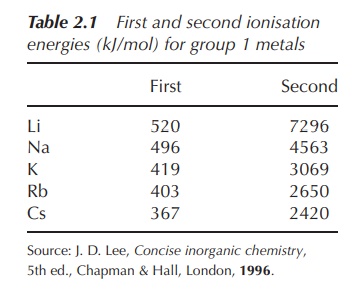
This group of elements belongs to the so-called s-block metals as they only have one electron in their outer shell, which is of s type. The chemistry of the metals is characterised by the loss of this s electron to form a monocationic ion M⁺, which results from the relatively low ionisation energy of this electron (Table 2.1).

The term ionisation energy (IE) is defined as the energy that is required to remove the outer electron of an atom or molecule. The tendency to lose the outer electron is directly correlated to the ionisation energy – the lower the ionisation energy, the easier the removal of the electron.

Within the group of alkali metals, the ionisation energy for the removal of the outer electron decreases as a result of the increasing distance of this electron from the nucleus.

The loss of the outer s electron within the group of alkali metals results in the formation of the M⁺ ion as mentioned. Consequently, most of the compounds of group 1 elements tend to be ionic in nature and form salts. In all pharmaceutical applications, only the salts of alkali metals are used, as most of the pure metals react violently with water.

1. Extraction of alkali metals: an introduction to redox chemistry

The main sources for Na and K are rock salts. Both elements do not naturally occur in their elemental state. In contrast, Li, Rb and Cs have small natural abundances, but also occur as rock salts. As previously mentioned, only artificial isotopes of Fr are known.

Sodium is manufactured by the so-called Downs’ process, which is the electrolysis of molten NaCl and represents the major production process for sodium metal and is also a minor source of industrial chlorine. The process is based on a redox reaction where the reduction of liquid Na⁺ to liquid Na takes place at the cathode and the oxidation of liquid chloride (Cl⁻) to chlorine (Cl₂) gas at the anode:

Reduction at the cathode ∶ Na⁺_(l)+ e⁻ → Na_(l)

Oxidation at the anode ∶ 2Cl⁻_(l) → Cl_2(g) + 2e⁻

                                       ^{----------------------------}

Overall redox reaction ∶ 2Na⁺_(l) + 2Cl⁻_(l)→ 2Na_(l) + Cl_2(g)

Molten NaCl is used as the electrolyte medium within the electrolytic Downs’ process and CaCl₂ is added in order to decrease the operating temperature. The melting point of NaCl is 800 ^∘C, whereas the addition of CaCl₂ lowers it to around 600 ^∘C. The design of the electrolysis cell is crucial in order to prevent oxidation and hydrolysis of freshly produced sodium and recombination to NaCl. Chlorine (Cl₂) is produced at the positive graphite anode and captured in form of gas, whereas Na⁺ is reduced to liquid sodium at the negative iron cathode and collected in its liquid form.

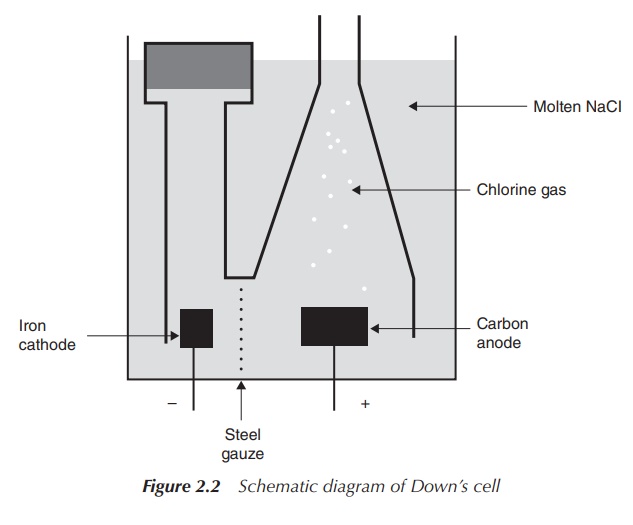
The anode is defined as the electrode at which the oxidation takes place, which, means in this example, that the anode is positively charged. Conversely, the cathode is defined as the place where the reduction takes place and therefore it is negatively charged in electrolysis processes. Note that the same definition for electrodes applies in a galvanic cell (e.g. in batteries), but as a result of the electron flow the anode has a negative charge whereas the cathode is positively charged (Figure 2.2).

Lithium can be isolated in a similar electrolytic process using lithium chloride (LiCl). Spodumene (LiAlSi₂O₆) is the main source for LiCl, which is reacted to LiOH by heating with CaO and subsequent conversion to LiCl prior to the electrolysis. Potassium can also be obtained via electrolysis of KCl, but there are more efficient methods, for example, the reaction to a Na-K alloy which can be subsequently distilled.

2. Excursus: reduction–oxidation reactions

The term redox (short for reduction–oxidation) reaction describes all chemical reactions in which atoms change their oxidation number. Redox reactions have many applications, which can range from industrial processes (see Downs’ process) to biological systems, for example, oxidation of glucose in the human body.

A redox reaction contains the two ‘half-reactions’, namely reduction and oxidation, which are always one set; this means that there is never a reduction reaction without an oxidation.

Redox reactions are a family of reactions that consist of oxidation and reduction reactions. These are always a matched set, that is, there is no oxidation reaction without a reduction reaction. They are called half-reactions, as two half-reactions are needed to form a redox reaction. Oxidation describes the loss of electrons (e⁻), whereas the term reduction is used for the gain of electrons (e⁻).

•       Reduction: Describes the gain of electrons or the decrease in the oxidation state of an atom or molecule.

•       Oxidation: Describes the loss of electrons or the increase in the oxidation state of an atom or molecule.

Reduction ∶ Fe → Fe²⁺ + 2e⁻

Oxidation ∶ Cu²⁺ → Cu + 2e⁻

Overall redox reaction ∶ Fe + Cu²⁺ → Fe²⁺ + Cu         (2.1)

Equation 2.1 gives an example for a simple redox reaction.

The terms oxidant and reductant are important terms used when discussing redox equations. An oxidant is defined as the atom or molecule that oxidises another compound and in turn is reduced itself. Reductants are molecules or atoms that reduce other compounds and as a result are oxidised themselves. Within a redox equation, there is always the oxidant–reductant pair present.

Reduction ∶ Oxidant + e⁻ → Product

Decrease in oxidation state (gain of electrons)

Oxidation ∶ Reductant  → Product + e⁻

Increase in oxidation state (loss of electrons)

Equation 2.2 shows the involvement of an oxidant and a reductant in redox reactions.

2.1 The oxidation state

It is actually not precisely correct to describe oxidation/reduction reactions as loss/gain of electrons. Both reactions are better referred to the changes in oxidation state rather than to the actual transfer of electrons; there are reactions classified as redox reaction even though no transfer of electrons takes place.

The oxidation state of an atom describes how many electrons it has lost whilst interacting with another atom compared to its original state (in its elemental form). The oxidation state is a hypothetical charge that an atom would have if all bonds within the molecule are seen as 100% ionic. When a bond is formed, it is possible for an atom to gain or lose electrons depending on its electronegativity. If an atom is elec-tropositive, it is more likely to take electrons away from another atom, and vice versa.

The oxidation number relates to the number of electrons that has been allocated to each atom; that is, if an atom has gained an electron, its oxidation state is reduced by 1 and therefore this atom has the oxidation state of –I.

IUPAC has defined the oxidation state as follows: A measure of the degree of oxidation of an atom in a substance. It is defined as the charge an atom might be imagined to have when electrons are counted according to an agreed-upon set of rules:

1.     The oxidation state of a free element (uncombined element) is zero.

2.     For a simple (monatomic) ion, the oxidation state is equal to the net charge on the ion.

3.     Hydrogen has an oxidation state of 1 and oxygen has an oxidation state of −2 when they are present in most compounds (exceptions to this are that hydrogen has an oxidation state of −1 in hydrides of active metals, e.g. LiH, and oxygen has an oxidation state of −1 in peroxides, e.g. H₂O₂).

4. The algebraic sum of the oxidation states of all atoms in a neutral molecule must be zero, whilst in ions the algebraic sum of the oxidation states of the constituent atoms must be equal to the charge on the ion. For example, the oxidation states of sulfur in H₂S, S₈ (elementary sulfur), SO₂, SO₃ and H₂SO₄ are, respectively: −2, 0, +4, +6 and +6. ‘The higher the oxidation state of a given atom, the greater its degree of oxidation; the lower the oxidation state, the greater its degree of reduction (Figure 2.3)’ .

2.2 How to establish a redox equation?

In order to describe the overall redox reaction, the establishing and balancing of the half-reaction is essential. In aqueous reactions, generally electrons, H⁺, OH⁻ and H₂O can be used to compensate for changes, whereas it has to be kept in mind whether the reaction takes place under acidic or basic conditions. There are five steps to follow in order to successfully establish a redox equation:

Example

Determine the redox equation for the reaction of MnO₄⁻ to Mn²⁺ and Ag to Ag⁺ under acidic conditions.

1. Determine the oxidation state of each element involved (oxidation number is stated in Roman numbers):

+VII −II               +II

MnO₄⁻ → Mn²⁺

0 +I

Ag  → Ag⁺

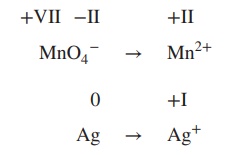
2. Add electrons to the equation; the number of electrons must reflect the changes in the oxidation state:

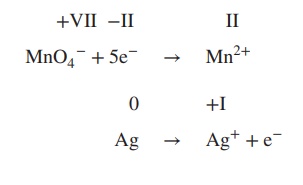
3. Determine which reaction is oxidation or reduction:

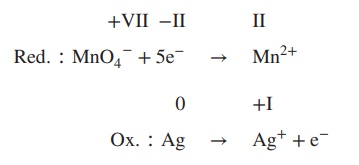
4. Balance reduction and oxidation reaction by using either H⁺/H₂O (acidic conditions) or OH⁻/H₂O (basic conditions), depending on the reaction conditions, which can be acidic or basic (in this example: acidic conditions):

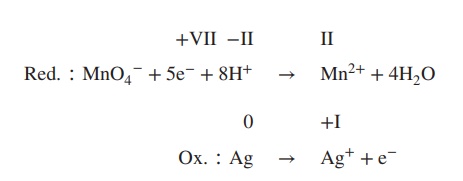
5. Formulate the redox equation keeping in mind that the number of electrons has to be equal in the reduc-tion and oxidation reactions. If necessary, the oxidation reaction has to be multiplied by the number of electrons in the reduction step, or vice versa.

Within the above example, the reaction conditions are stated as being acidic. A similar example using basic conditions is stated below and hydroxyl ions and water (OH⁻/H₂O) are used in order to balance the half-reactions.

Example

Determine the redox equation for the reaction of MnO₄⁻ to MnO₂ and Fe²⁺ to Fe³⁺ under basic conditions.

1. Determine the oxidation state of each element involved:

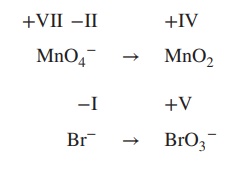
2. Add electrons to the equation; the number of electrons must reflect the changes in the oxidation state:

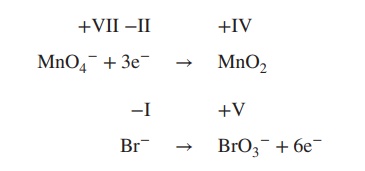
3. Determine the redox and the oxidation reaction:

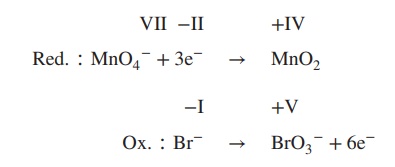
4. Balance reduction and oxidation reaction by using OH⁻/H₂O:

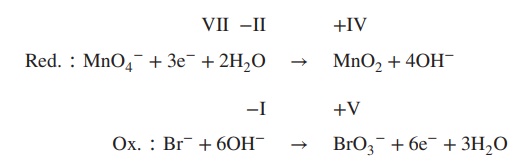
5. Formulate the redox equation:

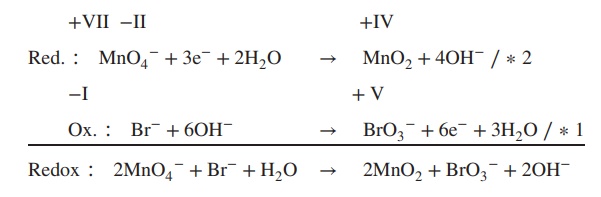
Redox ∶ 2MnO₄⁻ + Br⁻ + H₂O → 2MnO₂ + BrO₃⁻ + 2OH⁻

2.3 How to calculate the redox potential

The spontaneous reaction of Zn_(s) metal with Cu²⁺_(aq) from a Cu(II) solution is the prime example for a redox reaction.

Zn_(s) + Cu²⁺_(aq) → Zn²⁺_(aq) + Cu_(s)

In order to calculate the overall redox potential, it is important to formulate the individual half-equations as reductions first. The standard reduction potential E_red⁰ for each reaction can be taken from standard tables:

Cu²⁺_(aq) + 2e⁻ → Cu_(s)               E⁰_red= +0.340V

Zn²⁺_(aq) + 2e⁻ → Zn_(s)             E⁰_red= −0.763V

The half-equation with the more positive value is the reduction, whilst the other reaction is the oxidation. In this example, Cu²⁺ will be reduced to Cu whilst Zn_(s) metal will be oxidised to Zn²⁺. The standard potential E⁰ of an oxidation half-equation is the negative value of E_red⁰.

Reduction ∶ Cu²⁺ _(aq) + 2e⁻ → Cu_(s)                                   E_red⁰ = +0.340V

Oxidation ∶ Zn_(s) → Zn²⁺_(aq) + 2e⁻                                       E⁰_ox = −(−0.763V)

In order to calculate the voltage produced by an electrochemical cell (E_cell⁰), the potentials of all half-equations are added up.

E_cell⁰ = E_red⁰ + E_ox⁰

For the example above ∶ E_cell⁰ = 0.340 V + [−(−0.763 V)] = 1.103 V

If you deal with more complicated redox reactions and half-equations have to be multiplied because of the different numbers of electrons in each half-equation, the standard potential E⁰ will not be affected by these coefficients. Furthermore, it is important to note that the above calculations can be used only if both reaction partners are present in the same concentration. Concentration can have an effect, and the overall potential is then calculated by using the so-called Nernst equation.

Table 2.2 Table of standard reduction potential under acidic conditions at25 ^∘C

                                  E⁰ (V)

Li⁺ + e^- → Li           −3.05

K⁺ + e^- → K            −2.93

Ba²⁺ + 2e^- → Ba            −2.90

Na⁺ + e^- → Na            −2.71

Mg²⁺ + 2e^- → Mg            −2.37

Al³⁺ + 3e^- → Al            −1.66

Mn²⁺ + 2e^- → Mn            −1.18

Ga³⁺ + 3e^- → Ga            −0.53

Tl⁺ + e^- → Tl            −0.34

Fe²⁺ + 2e^- → Fe            −0.44

Cr³⁺ + 3e^- → Cr            −0.74

Cr³⁺ + e^- → Cr²⁺            −0.41

Ni²⁺ + 2e^- → Ni            −0.25

Cu²⁺ + e^- → Cu⁺            +0.15

Cu²⁺ + 2e^- → Cu            ⁺0.35

Cu⁺ + e^- → Cu            +0.50

I₂ + 2e^- → 2I ^-            +0.54

Fe³⁺ + e^- → Fe²⁺            +0.77

Br₂ + 2e^- → 2Br^-            +1.07

MnO₂ + 2e^- → Mn²⁺            +1.23

Cl₂ + 2e^- → 2Cl^-            +1.36

MnO₄^-+ 5e^- → Mn²⁺            +1.54

F₂ + 2e^- → 2F^-            +2.65

3. Chemical behaviour of alkali metals

Most alkali metals have a silvery white appearance with the exception of caesium which is golden yellow. They are all soft metals and typically can be cut with a knife. The softness of the metal increases within the group; caesium is the softest of the alkali metals.

Alkali metals are generally very reactive and oxidise in the air. The reactivity increases within the group, with lithium having the lowest reactivity and caesium the highest. Therefore, all alkali metals except lithium have to be stored in mineral oil. Lithium as an exception is normally stored under inert gas such as argon. Nevertheless, lithium, sodium and potassium can be handled in air for a short time, whereas rubidium and caesium have to be handled in an inert gas atmosphere.

All alkali metals react violently with water with the formation of the metal hydroxide and hydrogen. Again, lithium is the least reactive alkali metal and reacts ‘only’ quickly with water, whereas potassium, rubidium and caesium are more reactive and react violently with water.

2Li_(s) + 2H₂O → 2LiOH + H_2(g) ↑                      (2.3)

In terms of their pharmaceutical applications, alkali metals are not directly useable mainly because of their reaction behaviour in aqueous media. Nevertheless, alkali metal halides, some oxides, carbonates, citrates and other salts are of medicinal interest. NaCl and KCl solutions are important as oral rehydration salts, and KCl can also be used to treat potassium depletion.

In general, alkali metal halides can be prepared by the direct combination of the elements, that is, the reaction of an alkali metal with halogens. Alkali metal halides are very soluble in water, which is important for a potential pharmaceutical application, and partly soluble in organic solvents.

2M+X₂ →2MX                                  (2.4)

Alkali metal oxides can be synthesised by heating alkali metals in an excess of air. Thereby, the oxide, peroxide or superoxide formation can be observed depending on the metal.

4Li + O₂ → 2Li₂O       oxide formation

2Na + O₂ → Na₂O₂       peroxide formation

K+O₂ → KO₂                    superoxide formation                (2.5)

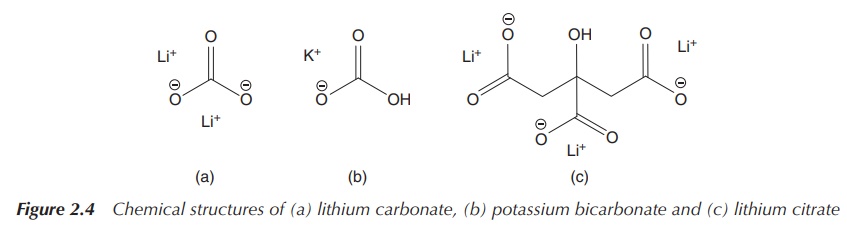
Alkali metal carbonates and bicarbonates have wide-ranging pharmaceutical applications. Lithium bicarbonate or citrate is used in the treatment of BD, whereas potassium bicarbonate or citrate is used in over-the-counter drugs as active pharmaceutical ingredients (APIs) against urinary-tract infections (increasing the pH of the urine) in the United Kingdom. Their solubility is highly dependent on the metal and varies from sparingly soluble (e.g. Li₂CO₃) whereas others are very soluble (Figure 2.4).

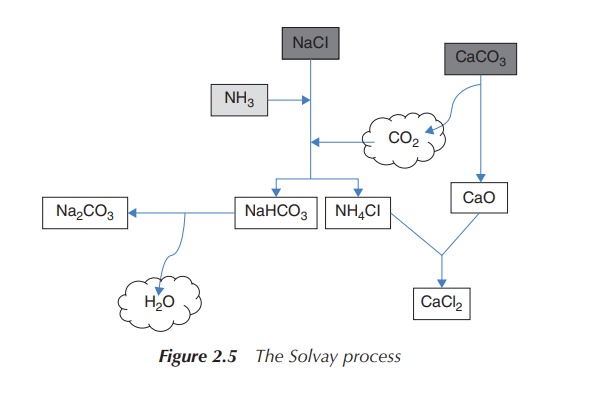
Sodium carbonate is produced by the so-called Solvay process – one of the most important industrial pro-cesses, which was developed in the 1860s by Ernest Solvay. Na₂CO₃ has extensive uses ranging from glass production to its application as a water softener. The starting materials, which are NaCl and CaCO₃ (lime stone), are inexpensive and easily available.

2NaCl + CaCO₃ → Na₂CO₃ + CaCl₂                            (2.6)

CaCO₃ is heated to around 1000 ^∘C, when it is converted to CO₂ and CaO (quicklime).

CaCO₃ → CO₂ + CaO                           (2.7)

CO₂ is then passed through an aqueous solution of NaCl and NH₃ (ammonia). NH₃ buffers the solution at a basic pH and NaHCO₃ (sodium bicarbonate) precipitates out of this solution. NaHCO₃ is less water soluble than NaCl at a basic pH. Without the addition of NH₃, the solution would be acidic, as HCl is produced as a by-product.

NaCl + CO₂ + NH₃ + H₂O → NaHCO₃ + NH₄Cl                      (2.8)

NaHCO₃ is filtered, and the remaining solution of NH₄Cl reacts with the CaO from step 1. The produced CaCl₂ is usually used as road salts, and NH₃ is recycled back to the initial reaction of NaCl (reaction step 2).

2NH₄Cl + CaO → 2NH₃ + CaCl₂ + H₂O                      (2.9)

In a final step, NaHCO₃ is converted to Na₂CO₃ (sodium carbonate) by calcination (heating to 160–230 ^∘C) with the loss of water.

2NaHCO₃ → Na₂CO₃ + H₂O + CO₂                                            (2.10)

Again, the CO₂ can be recycled and reused within the process. This means that the Solvay process consumes only a very small amount of NH₃ and the only ingredients are NaCl and CaCO₃ (Figure 2.5).

In terms of pharmaceutical applications, the various salts of sodium, lithium and potassium have the widest use and are discussed in detail in the following sections. These applications range from the use of sodium and potassium salts in dehydration solutions in order to restore replenished mineral balances to the treatment of BD with simple lithium salts.