Application of Dimensional Analysis to Convective Heat Transfer

APPLICATION OF DIMENSIONAL ANALYSIS TO CONVECTIVE HEAT TRANSFER

Dimensional analysis offers a rational approach to the estimation of the complex phenomena of convective heat transfer rates.

Free convection describes heat transfer by the bulk movement of fluids induced by buoyancy forces. These arise from the variation of fluid density with temperature. If the surface in contact with the fluid is hotter, the fluid will absorb heat, a local decrease in density will occur, and some of the fluid will rise. If the surface is colder, the reverse takes place. For these conditions, the fol-lowing factors will influence the heat transferred per unit area per unit time, q. The dimensional form of these factors is given, using the additional fundamental dimensions of temperature, [θ], and heat, [H]. The latter is justified if inter-change of heat energy and mechanical energy is precluded. This is approxi-mately true in the subject under discussion, the heat produced by frictional effects, for example, being negligible.

·       The viscosity of the fluid, η: [ML^-1T^-1]

·       The thermal conductivity of the fluid, k: [HT^-1L^-1θ^-1]

·       The temperature difference between the surface and the bulk of the fluid, ΔT:[θ]

·       The density, ρ: [ML^-3]

·       The specific heat, Cp: [HM^-1θ^-1]

·       The buoyancy forces. These depend on the product of the coefficient of thermal expansion, a, and the acceleration due to gravity, g: [θ^-1LT^-2]

Normally, only one dimension, of the physical dimensions of the surface, is important. For example, the height of a plane vertical surface has greater significance than the width that only determines the total area involved. The important characteristic dimension is designated l [L].

The equation of dimensions is then

[q] = [ l^x ΔT^y k^z η^p C^q_p (ag)r ρ ^s]

or

[HL^-2T^-1] = [L^xθ^yH^zT^-zL^-zθ^-zM^pL^-pT^-pH^qM^-qθ^-qθ^-rL^rT^-2rM^sL^-3s]

Equating indices,

H      1 = q + z

L      -2 = x - p + r - 3s - z

T      -1 = -p - 2r-  z

θ      0 = y - q - r - z, and

M      0 = p - q + s

Solving for x, y, z, p, and s in terms of q and r,

z = 1 - q

y = r + 1

p = q - 2r

s = 2r, and

x = 3r - 1

Therefore,

[q] = [ l^3r-1 ΔT^r+1C^q_pk^1-q (ag)^r ρ^{2r ηq} 2r]

Collecting into three groups, the variables to the power of one, the power, q, and the power, r, we can write

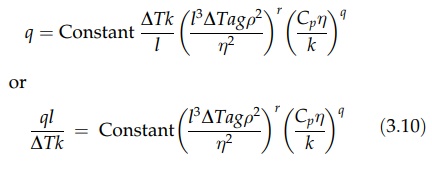
Heat transfer by free convection can thus be presented as a relation between three dimensionless groups. C_pη/k is known as the Prandtl number; the combination  l³ΔTagρ²/η² is known as the Grashof number; and ql/ΔTk is the Nusselt number. Since the film coefficient, h, is given by q/ΔT, the Nusselt number may also be written as hl/k.

The specific relation in which these groups stand is established for a particular system by experiment. Then, for the same geometric arrangement, in which heat is transferred by free convection, the correlation allows the Nusselt number, Nu, to be determined with reasonable accuracy from known values of the variables that constitute the Grashof number, Gr, and the Prandtl number, Pr. From Nu, the heat transferred per unit area per unit time, q, and the film coefficient, h, can be determined.

The fluid properties Cp, k, η, and ρ are themselves temperature dependent. In establishing a correlation, the temperature at which these properties are to be measured must be chosen. This is usually the temperature of the main body of the fluid or the mean of this temperature and the temperature of the surface.

Experimental correlations for many surface configurations are available. The exponents r and q are usually found to be equal to a value of 0.25 in streamline flow and 0.33 in turbulent flow. The constant varies with the physical configuration. As an example, the heat transfer to gases and liquids from a large horizontal pipe by free convection is described by the relation

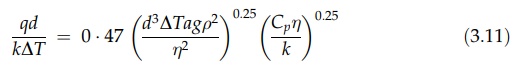
The linear dimension in this correlation is the pipe diameter, d. The fluid properties are to be measured at the mean of the wall and bulk fluid temper-atures.

In forced convection, the fluid is moved over the surface by a pump or blower. The effects of natural convection are usually neglected. The study of forced convection is of great practical importance, and a vast amount of data has been documented for streamline and turbulent flow in pipes, across and parallel to tubes, across plane surfaces, and in other important configurations such as jackets and coils. Such data is again correlated by means of dimensionless groups.

In forced convection, the heat transferred per unit area per unit time, q, is determined by a linear dimension, which characterizes the surface, l, the tem-perature difference between the surface and the fluid, ΔT, the viscosity, η, the density, ρ, and the velocity, u, of the fluid, its conductivity, k, and its specific heat, Cp. Dimensional analysis will yield the following relation:

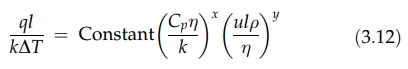
where ql/kΔT is the Nusselt number, Nu, and C_pη/k is the Prandtl number, Pr, and ulρ/η is Reynolds number, Re, a parameter discussed in chapter 2. The values of the indices, x and y, and of the constant are established for a particular system by experiment. In the case of turbulent flow in pipes, the correlation for fluids of low viscosity is

Nu = 0 023Pr^xRe^0:8                 (3:13)

where x has the values 0.4 for heating and 0.3 for cooling. The linear dimension used to calculate Re or Nu is the pipe diameter, and the physical properties of the fluid are to be measured at the bulk fluid temperature. This relation shows that in a given system, the film coefficient varies as the fluid velocity^0.8. If the flow velocity is doubled, the film coefficient increases by a factor of 1.7.

Although the correlations given above may appear complex, their use in practice is often simple. A large quantity of tabulated data is available, and numerical values of the variables and their dimensionless combinations are readily accessible. The graphical presentation of these variables or groups will, in many cases, permit an easy solution. In other cases, the correlation can be greatly simplified if it is restricted to a particular system. Free convection to air is an important example.