Heat Exchange Between a Fluid and a Solid Boundary
| Home | | Pharmaceutical Technology |Chapter: Pharmaceutical Engineering: Heat Transfer
Conduction and convection contribute to the transfer of heat from a fluid to a boundary.
HEAT EXCHANGE BETWEEN A FLUID AND A SOLID BOUNDARY
Conduction
and convection contribute to the transfer of heat from a fluid to a boundary.
The distribution of temperatures at a plane barrier separating two fluids is
shown in Figure 3.2. If the fluids are in turbulent motion, temperature
gradients are confined to a relatively narrow region adjacent to the wall.
Outside this region, turbulent mixing, the mechanism of which is explained in
chapter 2, is very effective in the transfer of heat. Temperature gradients are
quickly destroyed, and equalization of values T1 and T2
occurs. Within the region, there exists a laminar sublayer across which heat is
transferred by conduction only. The thermal conductivity of most fluids is
small, as shown in Table 3.1. The
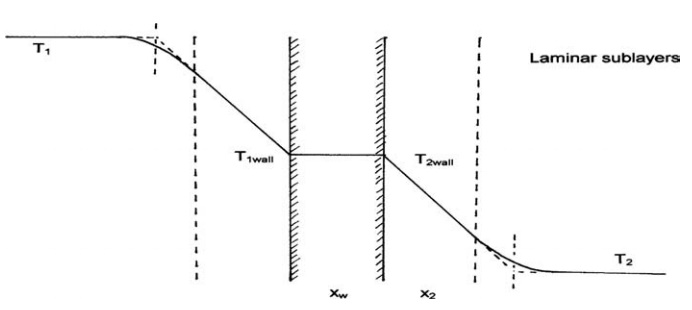
FIGURE 3.2 Heat transfer between fluids.
temperature
gradients produced by a given heat flow are correspondingly high. Outside the
laminar layer, eddies contribute to the transfer of heat by moving fluid from
the turbulent bulk to the edge of the sublayer, where heat can be lost or
gained, and by corresponding movements in the opposite direction. The
temperature gradients in this region, where both convection and conduction
contribute to heat transfer, are smaller than that in the sublayer.
The
major resistance to heat flow resides in the laminar sublayer. Its thickness
is, therefore, of critical importance in determining the rate of heat transfer
from the fluid to the boundary. It depends on the physical properties of the
fluid, the flow conditions, and the nature of the surface. Increase in flow
velocity, for example, decreases the thickness of the layer and, therefore, its
resistance to heat flow. The interaction of these variables is exceedingly
complex.
A
film transmitting heat only by conduction may be postulated to evaluate the
rate of heat transfer at a boundary. This fictitious film presents the same
resistance to heat transfer as the complex turbulent and laminar regions near
the wall. If, on the hot side of the wall, the fictitious layer had a thickness
x1, the equation of heat transfer to the wall would be
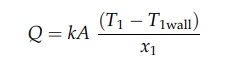
where
k is the thermal conductivity of the
fluid. A similar equation will apply to heat transfer at the cold side of the
wall. The thickness of the layer is determined by the same factors that control
the extent of the laminar sublayer. In general, it is not known and the
equation above may be rewritten as
Q
= h1A(T1 - T1wall) (3:7)
where
h1 is the heat transfer
coefficient for the film under discussion. It corre-sponds to the ratio k/x1 and has units J/m2·sec·K.
This is a convenient, numerical expression of the flow of heat by conduction
and convection at a boundary. Typical values of heat transfer or film
coefficients are given in Table 3.2. The approximate evaluation of these
coefficients is discussed in the next section.
The
ratio of the temperature difference and the total thermal resistance determines
the rate of heat transfer across the three layers of Figure 3.2. Using the film
coefficient h2 to characterize heat transfer from the barrier to the
colder fluid,
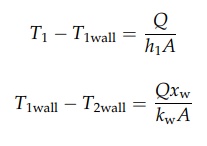
TABLE 3.2 Film Coefficient, h, for Various Fluids (J/m2 sec K)

where
kw is the thermal
conductivity of the wall.
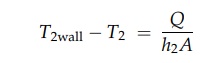
Addition
and rearrangement of these equations give
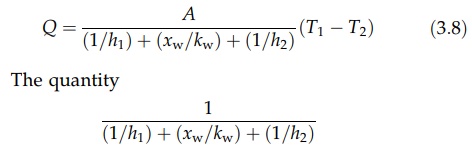
is
called the overall heat transfer coefficient, U. A general expression of the
rate of heat transfer then becomes
Q
= UAΔT (3:9)
Related Topics
