Heat Transfer Through a Wall

HEAT TRANSFER THROUGH A WALL

Heat transfer by conduction through walls follows the basic relation given by Fourier’s equation in which the rate of heat flow, Q, is proportional to the temperature gradient, dT/dx, and to the area normal to the heat flow, A.

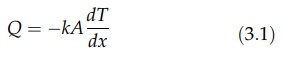
As the distance, x, increases, the temperature, T, decreases. Hence, measuring in the x direction, the temperature gradient, dT/dx, is algebraically nega-tive. The proportionality constant, k, is the thermal conductivity. Its numerical value depends on the material of which the body is made and on its temperature.

Values of thermal conductivity, k, for a number of materials are given in Table 3.1.

Metals have high conductivity, although values vary widely. The non-metallic solids normally have lower conductivities than metals. For the porous materials of this group, the overall conductivity lies between that of the homogeneous solid and the air that permeates the structure. Low resultant values lead to their wide use as heat insulators. Carbon is an exception among nonmetals. Its relatively high conductivity and chemical inertness permit its wide use in heat exchangers.

TABLE 3.1 Thermal Conductivity, k, of Various Materials (in J/sec m K)

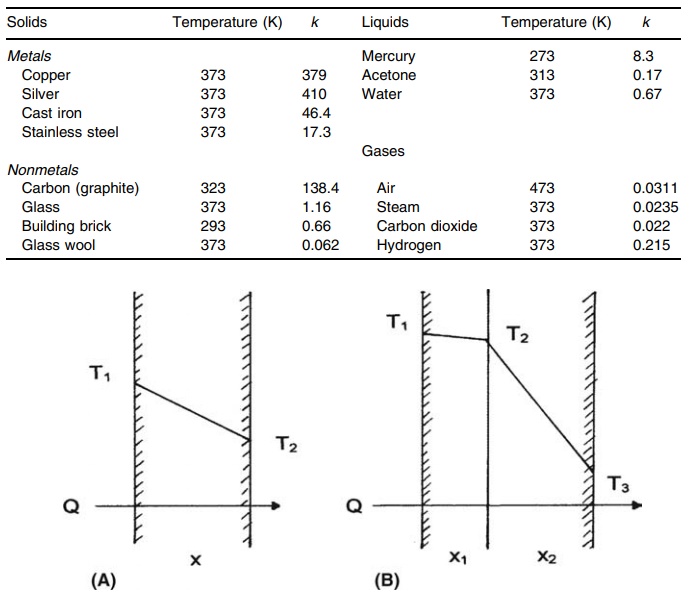
FIGURE 3.1 Conduction of heat through a wall.

Steady nondirectional heat transfer through a plane wall of thickness x and area A is represented in Figure 3.1A. Assuming that the thermal conductivity does not change with temperature, the temperature gradient will be linear and equal to (T₁ T₂)/x, where T₁ is the temperature of the hot face and T₂ is the temperature of the cool face. Equation (3.1) then becomes

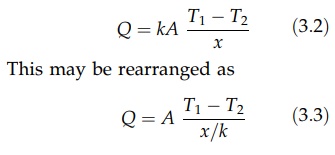
where x/k is the thermal resistance. Thus, for a given heat flow, a large temperature drop must be created if the wall or layer has a high thermal resistance.

An increase in thermal resistance will reduce the heat flow promoted by a given temperature difference. This is the principle of insulation by lagging, and it is illustrated by a composite wall shown in Figure 3.1B. The rate of heat transfer will be the same for both materials if steady-state heat transfer exists. Therefore,

The major temperature drop occurs across the distance x₂ since this material provides the major thermal resistance. (In the case of heavily lagged, thin metal walls, the temperature drop and thermal resistance of the metal are so small that they can be ignored.) Rearrangement of this equation and the elimi-nation of the junction temperature give

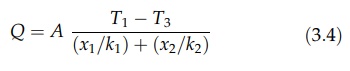
Equations of this form can be applied to any number of layers.