Motion of Bodies in a Fluid

MOTION OF BODIES IN A FLUID

When a body moves relative to a fluid in which it is immersed, resistance to motion is encountered and a force must be exerted in the direction of relative body movement. The opposing drag force is made up from two components, viscous drag and form drag. This may be explained by reference to Figure 2.11, which describes the flow past a body, in this case, a cylinder with axis normal to the page, by means of streamlines. As mentioned, streamlines are hypothetical lines drawn tangential at all points to the motion of the fluid. Flow past the cylinder immobilizes the fluid layer in contact with the surface, and the induced velocity gradients result in shear stress or viscous drag on the surface. The crowding of streamlines on the upstream face of the cylinder, the flow pattern, and momentum changes on the downstream surface must be exactly reversed. This is shown in Figure 2.11A, and the entire force opposing relative motion of the cylinder and fluid is viscous drag. However, conditions of increasing pressure and decreasing velocity that exist on the downstream surface may cause the boundary layer to separate. The region between the breakaway streamlines—the wake—is occupied by eddies and vortices, and the flow pat-tern shown in Figure 2.11B is established. The kinetic energy of the accelerated fluid is dissipated and not recovered as pressure energy on the downstream surface. Under these conditions, there is a second component to the force opposing relative motion. This is known as form drag. Its contribution to the total drag increases as the velocity increases.

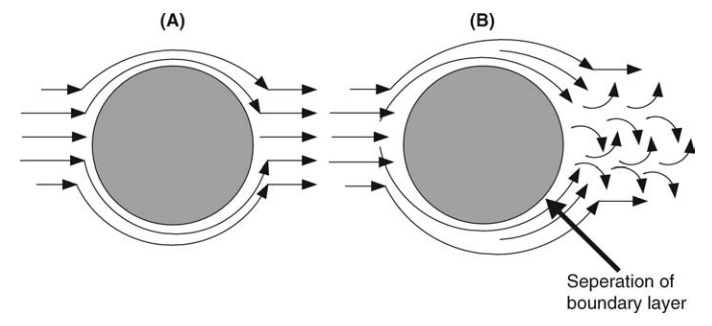
FIGURE 2.11 Flow of fluid past a cylinder (A) laminar and (B) turbulent.

Once again, viscous and inertial forces are operating to determine the flow pattern and drag force on a body moving relative to a fluid. Reynolds number, which expresses their ratio, is used as a parameter to predict flow behavior. The relation between the drag force and its controlling variables is presented in a manner similar to that employed for flow in a pipe. If we consider a sphere moving relative to a fluid, the projected area normal to flow is πd²/4, where d is the diameter of the sphere. The drag force acting on the unit projected area, R^’, is determined by the velocity, u, the viscosity, η, and the density, ρ, of the fluid, and the diameter of the sphere, d. Dimensional analysis yields the relation

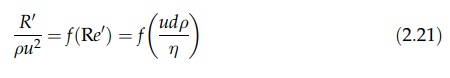
The form of Reynolds number, Re^’, employs the diameter of the sphere as the linear dimension. With the exception of an analysis at very low Reynolds numbers, the form of this function is established by experiment. Results are presented on logarithmic coordinates in Figure 2.12. When Re^’ ≤ 0.2, viscous forces are solely responsible for drag on the sphere and equation (2.21) is

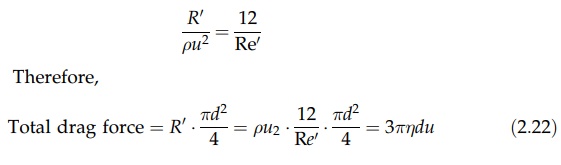
This is the normal form of Stokes’ law.

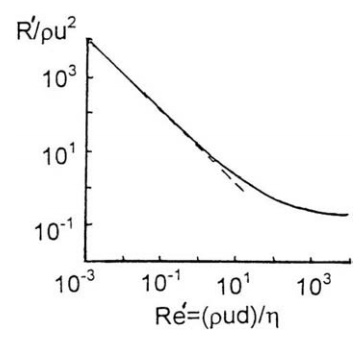
FIGURE 2.12 R^’/ρμ² versus Reynolds number for a smooth sphere.

At larger Re^’ values, the experimental curve progressively diverges from this relation, ultimately becoming independent of Re⁰ and giving a value of R^’/ρu² = 0.22. As Re^’ increases, the form drag increases, ultimately becoming solely responsible for the force opposing motion.

For nonspherical particles, the analysis employs the diameter of a sphere of equivalent volume. A correction factor, which depends on the shape of the body and its orientation in the fluid, must be applied.

An important application of this analysis is the estimation of the speed at which particles settle in a fluid. Under the action of gravity, the particle accel-erates until the weight force, mg, is exactly balanced by the opposing drag. The body then falls at a constant terminal velocity, u. Equating weight and drag forces gives

where ρ is the density of the particle.

For a sphere falling under streamline conditions (Re^’ < 0.2), R^’ = ρu²·12/ Re^’. Substituting in equation (2.23), we obtain

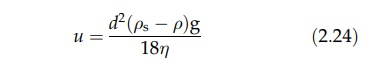
This expression follows more simply from the equation mg - 3πdηu.