Liquid Flow in Pipes
| Home | | Pharmaceutical Technology |Chapter: Pharmaceutical Engineering: Fluid Flow
The many pharmaceutical processes that involve the transfer of a liquid confer great importance on the study of flow in pipes.
LIQUID FLOW IN PIPES
The many
pharmaceutical processes that involve the transfer of a liquid confer great
importance on the study of flow in pipes. This study permits the evalu-ation of
pressure loss due to friction in a simple pipe and assesses the additional
effects of pipe roughness, changes in diameter, bends, exists, and entrances.
When the total pressure drop due to friction is known for the system, the
equivalent head can be derived and the power requirement for driving a liquid
through the system can be calculated from equation (2.14).
Streamline Flow in a Tube
The
mathematical analysis of streamline flow in a simple tube results in the
expression known as Poiseuille’s law, one form of which is equation (2.14):
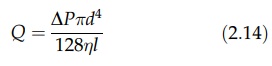
where Q is the
volumetric flow rate or discharge, ΔP is the pressure drop across the
tube, d and l are the diameter and length of the tube, respectively, and η is
the viscosity of the fluid.
Whether
flow in the tube is streamline or turbulent, an infinitesimally thin stationary
layer is found at the wall. The velocity increases from zero at this point to a
maximum at the axis of the tube. The velocity profile of streamline flow is
shown in Figure 2.9A. The velocity gradient du/dr
is seen to vary from a maximum at the wall to zero at the axis. In flow through
a tube, the rate of shear is equal to the velocity gradient, and equation (2.1)
dictates the same variation of shear stress.
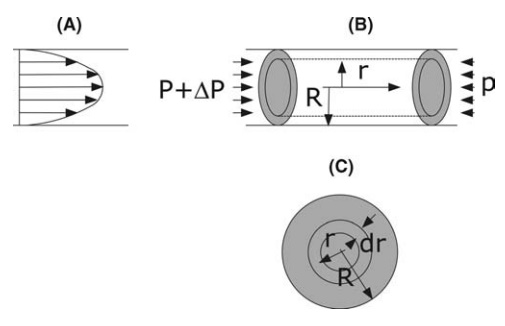
FIGURE 2.9 Streamline flow. (A) Velocity profile in a pipe; (B) longitudinal terms
and (C) cross-sectional terms used to define flow properties.
To
derive Poiseuille’s law, the form of the velocity profile must first be
established. For a fluid contained within a radius r flowing in a tube of
radius R, this is shown in Figure 2.9B. If the pressure drop across length l is
ΔP, the force
attributed to the applied pressure driving this section is ΔPpr2. If
the flow is steady, this force can only be balanced by opposing viscous forces
acting on the “wall” of the section. This force, the product of the shear
stress t and the area over
which it acts, is 2tπl.
The expression given by equating these forces is
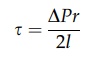
Substituting
from equation (2.1) gives
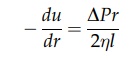
The
velocity gradient is negative because u
decreases as r increases. When r = R, u = 0. Integration
gives
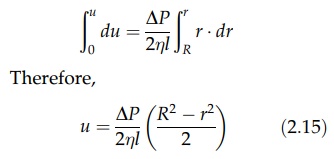
This
relation shows that the velocity distribution across the tube is parabolic. For
such a distribution, the maximum velocity is twice the mean velocity. The
volumetric flow rate across an annular section between r and (r + dr) shown in Figure 2.9C is
Q
= 2πr.dr. r
Substituting
for u from equation (2.15) gives
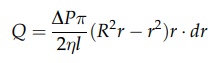
The
total volumetric flow rate is the integral between the limits r = R and r = 0:
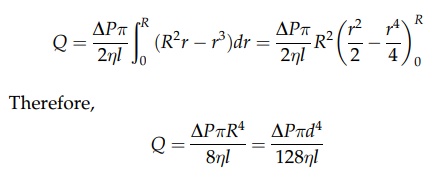
which
is equation (2.14), where d is the diameter of the tube. Since Q = umeanp(d2/ 4), substitution and
rearrangement gives

Dimensional Analysis and Flow
Through a Tube: A General Approach
The
utility of equation (2.16) for evaluating the loss of pressure due to friction
in a tube is limited because streamline conditions are rare in practice. The
theo-retical analysis of turbulent flow, however, is incomplete, and
experiments with fluids are necessary for the development of satisfactory
relations between the controlling variables, one in terms of the other, while
other variables are tem-porarily held constant. Dimensional analysis is a
procedure in which the interaction of variables is presented in such a way that
the effect of each variable can be assessed.
The
method is based on the requirement that the dimensions of all terms of a
physically meaningful equation are the same, that is, an equation must be
dimensionally homogeneous. This principle may be usefully illustrated by
ref-erence to equation (2.14) written in the form
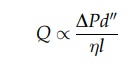
Reviewing
in basic units of mass, length, and time and using the symbol [ ] to represent
dimension of [Q] = [L3T-1],
[ΔP] = [ML-1T-2], [dn]
= [Ln],
and [η] = [M L-1T-1],
equating gives
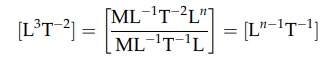
[M]
and [T] are correct, as they must be. Equating [L] gives [L3] = [Ln-1] from which n = 4.
If
no previous knowledge of the combined form of the variable that determines Q is
available, dimensional analysis can be applied in the following way. The
dependence of Q on ΔP,
l, d, and η
can be written as
Q
= f(ΔP; l; d; η)
The
function f can be expressed as a
series, each term of which is the product of the independent variables raised
to suitable powers. Taking the first term of the series gives
Q
= N . ΔPw . Lx
. Dy . ηz
where
N is a numerical factor (dimensionless). Rewriting terms as [Q] = [L3T-1], [ΔPw] = [MwL-wT-2w],
[lx] = [Lx], [dy] = [Ly], and [ηz] = [MzL-zT-z],
the equation [Q] = [ΔPw·lx·Dy·ηz] becomes [L3T-1]
= [MwL-wT-2w·Lx·Ly·MzLzT-z].
Equating
powers of M, L, and T gives the following system:
M:0
= w + z
L
: 3 = -w + x + y - z
T:
- 1 = - 2w - z
Since
four unknowns are present in three simultaneous equations, three may be determined
in terms of the fourth. Solving gives w = l, z = -1, and x + y
= 3.
Expressing
y as 3’ - x, one gets
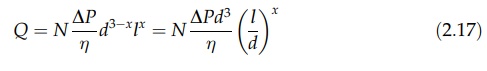
The
first part of the example demonstrates the use of dimensions as a partial check
on the derivation or completeness of a solution. In the second part, a
solution, although incomplete, gives considerable information about discharge
of a fluid in streamline flow and its relation to pressure drop, viscosity, and
the geometry of the pipe without any theoretical or experimental analysis. For
example, if two tubes had the same ratio l/d,
the values of Q/ηd3ΔP would also be the same.
Since
the exponent x in equation (2.17) is
indeterminate, the term in brackets must be dimensionless. Unlike the lengths
from which it is derived, it is a pure number and needs no system of units for
meaningful expression. Its value is, therefore, independent of the units chosen
for its measurement, provided, of course, that the systems of measurement are
not mixed. The equation may, therefore, be presented as the relation between
two dimensionless groups as
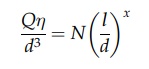
or,
since a series of power terms will, in general, form the original unknown
function, each of which has different values of N and x,
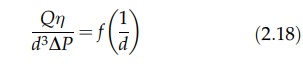
The
study of frictional losses at the wall of a pipe is facilitated by dimensional
analysis. The shear stress—that is, the force opposing motion of the fluid
acting on each unit of area of the pipe, R—is
determined for a given pipe surface by the velocity of the fluid, u, the diameter of pipe, d, the viscosity of the fluid, η, and the fluid density, ρ. The equation of dimensions is
[R]
= [uo dq ηy ρs]
Therefore,
ML-1T-2
= LpT-p . Lq
. M1L-rT-r . MsL-3s
Equating
M, L, and T, one gets
M:
1 = r + s
L:
-1 = p + q - r - 3s
T:
-2 = - p - r
Solving
for p, r, and s in terms of q gives r = -q,
s = 1 + q, and p = 2 + q.
Therefore,
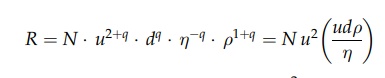
where
N is a numerical factor. Generalizing, R/ρu2, which is the
friction factor, is a function of a dimensionless combination of u, d,
η, and ρ. This combination gives a parameter
known as the Reynolds number, Re. Therefore,
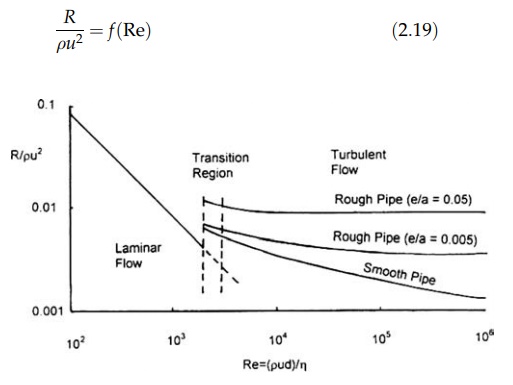
FIGURE 2.10 Pipe friction chart: R/ρμ2
versus Reynolds number.
In
turbulent flow, the shear stress at the wall depends on the surface, the value
being higher for a rough pipe than for a smooth pipe when flow conditions are
otherwise the same. Equation (2.19) therefore yields a family of curves when
pipes are of differing dimensionless group, e/a,
in which e is a linear dimension
expressing roughness. Values of e are
known for many materials.
The
complete dimensionless correlation, plotted on logarithmic coor-dinates so that
widely varying conditions are covered, is given in Figure 2.10. The curve can
be divided into four regions. When Re < 2000, flow is streamline and the
equation of the line in this region is R/ρu2 = 8/Re. This is simply another form
of Poiseuille’s law. The friction factor is independent of the roughness of the
pipe, and all data fall on a single line.
When
Re lies between 2000 and 3000, flow normally becomes turbulent. The exact value
of the transition depends on the idiosyncrasies of the system. For example, in
a smooth pipe, streamline conditions will persist at higher Reynolds number
than in a pipe in which disturbances are created by surface roughness.
At
higher values of Re, flow becomes increasingly turbulent to give a region in
which the friction factor is a function of Re and surface roughness.
Ultimately, this merges with a region in which the friction factor is
independent of Re. Flow is fully turbulent, and for a given surface, the shear
stress at the pipe wall is proportional to the square of the fluid velocity.
The onset of the fourth region occurs at a lower Re in rough pipes.
The
essential difference between laminar flow and turbulent flow has already been
described. In a pipe, the enhanced momentum transfer of the latter modifies the
velocity distribution. In laminar flow, this distribution is parabolic. In
turbulent flow, a much greater equalization of velocity occurs, the velocity
profile becomes flatter, and high-velocity gradients are confined to a region
quite close to the wall. In both cases, the boundary layer, the region in which
flow is perturbed by the presence of the boundary, extends to the pipe axis and
completely fills the tube. In laminar conditions, the structure of the layer is
quite simple, layers of fluid sliding one over another in an orderly fashion.
In tur-bulent flow, however, division can be made into three regimes: (i) the
core of fluid, which is turbulent; (ii) a thin layer at the wall, which is a
millimeter thick and where laminar conditions persist; this is called the
laminar sublayer, and it is separated from the turbulent core by (iii) a buffer
layer in which transition from turbulent flow to laminar flow occurs.
This
description of the turbulent boundary layer applies generally to the flow of
fluids over surfaces. The properties of this layer are central in many aspects
of the flow of fluids. In addition, these properties determine the rate at
which heat or mass is transferred to or from the boundary. These subjects are
described in chapters 3 and 4.
Related Topics
