The Measure of Pressure Intensity

THE MEASURE OF PRESSURE INTENSITY

Application of equation (2.3) to the column of liquid shown in Figure 2.3A gives

P_A - P₁ = -ρgh

and

P₁ = P_A + ρgh                      (2:4)

The density term should be the difference between the density of the liquid in the column and the density of the surrounding air. The latter is relatively small, and this discrepancy can be ignored. P₁ is the absolute pressure at the point indicated, and P_A is the atmospheric pressure. It is often convenient to refer to the pressure measured relative to atmospheric pressure, that is, P₁ - P_A. This is called the gauge pressure and is equal to ρgh. SI unit for pressure is N/m². Alternatively, the gauge pressure can be expressed as the height or head of a static liquid that would produce pressure.

Figure 2.3A represents the simplest form of a manometer, a device widely used for the measurement of pressure. It consists of a vertical tube tapped into the container of the fluid being studied. In this form, it is confined to the

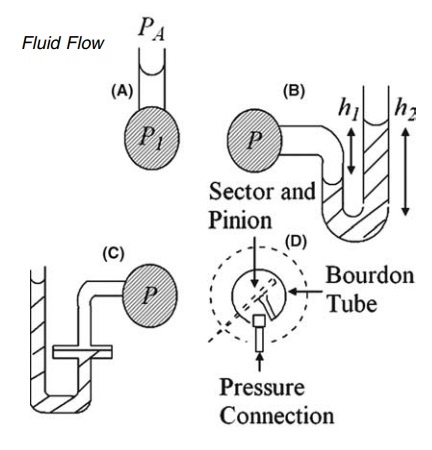
FIGURE 2.3 Pressure measurement apparatus (A) vertical; (B) U-tube; (C) modified U-tube manometers and (D) Bourdon gauge.

pressure measurement of liquids. This device is unsuitable for the measurement of very large heads, because of unwieldy construction, or very small heads, because of low accuracy. The U-tube manometer, shown in Figure 2.3B, may be used for the measurement of higher pressures with both liquids and gases. The density of the immiscible liquid in the U-tube, ρ₁, is greater than the density of the fluid in the container, ρ₂. The gauge pressure is given by

P = h₁ρ₁g - h₂ρ₂g

The disadvantage of reading two levels may be overcome by the modification in Figure 2.3C. The cross-sectional area of one limb is many times larger than that of the other, and the vertical movement of the heavier liquid in the wider arm can be neglected and its level is assumed to be constant.

Sloping the reading arm of the manometer can increase the accuracy of the pressure determination for small heads with any of the manometers just described. The head is now derived from the distance moved along the tube and the angle of the slope.

The Bourdon gauge, a compact instrument widely used for the measure-ment of pressure, differs in principle from the manometer. The fluid is admitted to a sealed tube of oval cross section, the shape of which is shown in Figure 2.3D. The straightening of the tube under internal pressure is opposed by its elasticity. The movement to an equilibrium position actuates a recording mechanism. The gauge is calibrated by an absolute method of pressure measurement.

The principles of pressure measurement also apply to fluids in motion. However, the presence of the meter should minimize perturbation in flow. A calming section, in which a flow regime becomes stable, is present upstream from the pressure tapping, and the edge of the latter should be flush with the inside of the container to prevent flow disturbance.

FIGURE 2.4 Flow of a fluid past a cylinder.