Fluid Flow

Fluid Flow

INTRODUCTION

Fluid flow is an essential element of many pharmaceutical processes. The ability to propel fluids through pipes and to direct materials from one location to another is central to the successful manufacture of many products. Fluids (liq-uids and gases) are a form of matter that cannot achieve equilibrium under an applied shear stress but deform continuously, or flow, as long as the shear stress is applied.

Viscosity

Viscosity is a property that characterizes the flow behavior of a fluid, reflecting the resistance to the development of velocity gradients within the fluid. Its quantitative significance may be explained by reference to Figure 2.1. A fluid is contained between two parallel planes each of area A m² and distance h m apart. The upper plane is subjected to a shear force of F N and acquires a velocity of u m/sec relative to the lower plane. The shear stress, t, is F/A N/m². The velocity gradient or rate of shear is given by u/h or, more generally, by the differential coefficient du/dy, where y is a distance measured in a direction perpendicular to the direction of shear. Since this term is described by the units velocity divided by a length, it has the dimension T^-1 or, in this example, reciprocal seconds. For gases, simple liquids, true solutions, and dilute disperse systems, the rate of shear is proportional to the shear stress. These systems are called Newtonian, and we can write

F/A = t =  η du/dy                   (2:1)

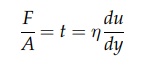
The proportionality constant η is the dynamic viscosity of the fluid: the higher its value, the lower the rates of shear induced by a given stress. The dimensions of dynamic viscosity are M L^-1 T^-1. For the SI system of units, viscosity is expressed in N·sec/m². For the centimeter-gram-second (CGS) sys-tem, the unit of viscosity is poise (P). One N·sec/m² is equivalent to 10 P. The viscosity of water at room temperature is about 0.01 P or 1 centipoise (cP). Pure glycerin at this temperature has a value of about 14 P. Air has a viscosity of 180 x 10^-6 P.

Complex disperse systems fail to show the proportionality described by equation (2.1), the viscosity increasing or, more commonly, decreasing with increase in the rate of shear. Viscosity may also depend on the duration of shear and even on the previous treatment of the fluids. Such fluids are termed non-Newtonian.

Equation (2.1) indicated that wherever a velocity gradient is induced within a fluid, a shear stress will result. When the flow of a fluid parallel to some boundary is considered, it is assumed that no slip occurs between the boundary and the fluid, so the fluid molecules adjacent to the surface are at rest (u = 0). As

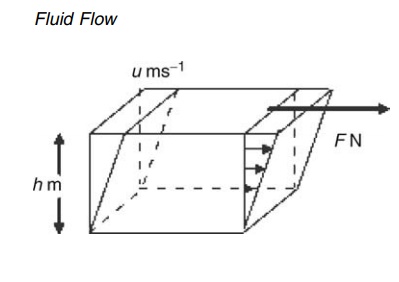
FIGURE 2.1 Schematic of fluid flow depicting the applied force, velocity in the direction of motion, and thickness of the fluid.

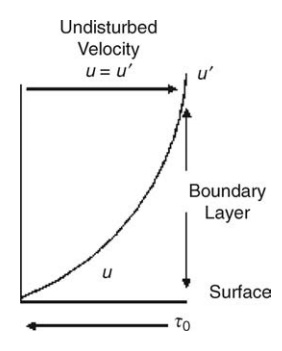
FIGURE 2.2 Distribution of velocities at a boundary layer.

shown in Figure 2.2, the velocity gradient du/dy decreases from a maximum at the boundary (y = 0) to zero at some distance from the boundary (y = y^’) when the velocity becomes equal to the undisturbed velocity of the fluid (u = u^’). The shear stress must, therefore, increase from zero at this point to a maximum at the boundary. A shear stress, opposing the motion of the fluid and sometimes called fluid friction, is therefore developed at the boundary. The region limited by the dimension y^’, in which flow of the fluid is perturbed by the boundary, is called the boundary layer. The structure of this layer greatly influences the rate at which heat is transferred from the boundary to the fluid under the influence of temperature gradient or the rate at which molecules diffuse from the boundary into the fluid under a concentration gradient. These topics are discussed in chapters 3 and 4.

Compressibility

Deformation is not only a shear-induced phenomenon. If the stress is applied normally and uniformly over all boundaries, then fluids, like solids, decrease in volume. This decrease in volume yields a proportionate increase in density. Liquids can be regarded as incompressible, and changes of density with pres-sure can be ignored, with consequent simplification of any analysis. This is not possible in the study of gases if significant changes in pressure occur.

Surface Tension

Surface tension, a property confined to a free surface and therefore not applicable to gases, is derived from unbalanced intermolecular forces near the surface of a liquid. This may be expressed as the work necessary to increase the surface by unit area. Although not normally important, it can become so if the free surface is present in a passage of small-diameter orifice or tube. Capillary forces, determined by the surface tension and the curvature of the surface, may then be comparable in magnitude to other forces acting in the fluid. An example is found in the movement of liquid through the interstices of a bed of porous solids during drying.