Flow Measurement

FLOW MEASUREMENT

The Bernoulli theorem can also be applied to the measurement of flow rate. Consider the passage of an incompressible fluid through the constriction shown in Figure 2.6. The increase in kinetic energy as the velocity increases from u₁ to u₂ is derived from the pressure energy of the fluid, the pressure of which drops from P₁ to P₂, the latter being recorded by manometers. There is no change in height, and equation (2.5) can be rearranged to give

The volumetric flow rate Q = u₁a₁ = u₂a₂. Therefore, by rearrangement,

This derivation neglects the correction of kinetic energy loss due to non-uniformity of flow in both cross sections and the frictional degradation of energy during passage through the constriction. This is corrected by the introduction of a numerical coefficient, C_D, known as the coefficient of discharge. Therefore,

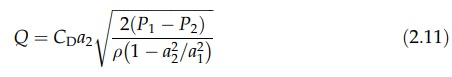
The value of C_D depends on conditions of flow and the shape of the constriction. For a well-shaped constriction (notably circular cross section), it would vary between 0.95 and 0.99 for turbulent flow. The value is much lower in laminar flow because the kinetic energy correction is larger. The return of the fluid to the original velocity by means of a diverging section forms a flow-measuring device known as a Venturi meter.

The Venturi meter is shown in Figure 2.7A. The converging cone leads to the narrowest cross section, known as the throat. The change in pressure is measured across this part of the meter and the volumetric flow rate is found by substitution into equation (2.11). Values of the coefficient of discharge are given in the preceding paragraph. The diverging section or diffuser is designed to induce a gradual return to the original velocity. This minimizes eddy formation in the diffuser and permits the recovery of a large proportion of the increased kinetic energy as pressure energy. The permanent loss of head due to friction in both converging and diverging sections is small. The meter is therefore efficient.

When the minimization of energy degradation is less important, the gradual, economic return to the original velocity may be abandoned, compen-sation for loss of efficiency being found in a device that is simpler, cheaper, and more adaptable than the Venturi meter. The orifice meter, to which this state-ment applies, consists simply of a plate with an orifice. A representation of flow through the meter is depicted in Figure 2.7B, indicating convergence of the fluid stream after passage through the orifice to give a cross section of minimum area called the vena contracta. The downstream pressure tapping is made at this cross section. 

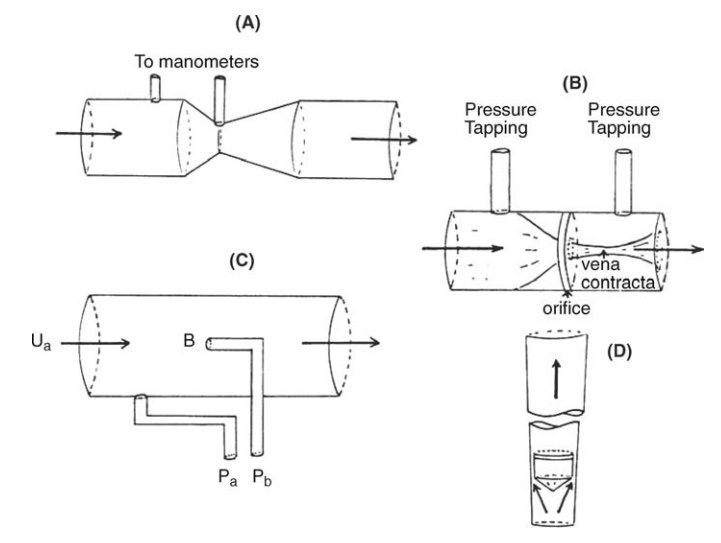
FIGURE 2.7 Flow meters: (A) Venturi meter, (B) orifice meter, (C) Pitot tube, and (D) rotameter.

The volumetric flow rate would be given by equation (2.6) for which a₂ is the jet area at the vena contracta. The measurement of this dimension is inconvenient. It is therefore related to the area of the orifice, a₀, which can be accurately measured by the coefficient of contraction, C_c, defined by the relation

C_c = a₂/a₀

The coefficient of contraction, frictional losses between the tapping points, and kinetic energy corrections are absorbed in the coefficient of discharge. The volumetric flow rate is then

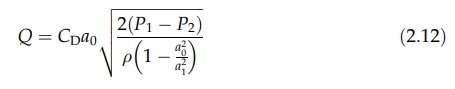
The term [1 - (a₀²/a₁²)] approaches unity if the orifice is small compared to the pipe cross section. Since P₁ - P₂ = Δhρg, Δh being the difference in head developed by the orifice, equation (2.12) reduces to

Q = C_D a₀ (2Δhg)^1/2                           (2:13)

The value of C_D for the orifice meter is about 0.6, varying with construction, the ratio a₀/a₁, and flow conditions within the meter. Because of its complexity, it cannot be calculated. After passage through the orifice, flow disturbance during retardation causes the dissipation of most of the excess kinetic energy as heat. The permanent loss of heat is therefore high, increasing as the ratio of a₀/a₁ falls, ultimately reaching the differential head produced within the meter. When constructional requirements and methods of installation are followed, the cor-recting coefficients can be derived from charts. Alternatively, the meters can be calibrated.

The Bernoulli theorem may be used to determine the change in pressure caused by retardation of fluid at the upstream side of a body immersed in a fluid stream. This principle is applied in the Pitot tube, shown in Figure 2.7C. The fluid velocity is reduced from u_a, the velocity of the fluid filament in alignment with the tube, to zero at B, a position known as the stagnation point. The pressure, P_b, is measured at this point by the method shown in Figure 2.7C. The undisturbed pressure, P_a, is measured in this example with a tapping point in the wall connected to a manometer. Since the velocity at B is zero, equation (2.10) reduces to

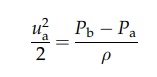
and u_a can be calculated. Since only a local velocity is measured, variation of velocity in a section can be studied by altering the position of the tube. This procedure must be used if the flow rate in a pipe is to be measured. The mean velocity is derived from velocities measured at different distances from the wall. This derivation and the low pressure differential developed render the Pitot tube less accurate than either the Venturi tube or the orifice meter for flow measure-ment. However, the tube is small in comparison with the pipe diameter and therefore produces no appreciable loss of head.

The rotameter (a variable area meter), shown in Figure 2.7D, is commonly used, giving a direct flow rate reading by the position of a small float in a vertical, calibrated glass tube through which the fluid is flowing. The tube is internally tapered toward the lower end so that the annulus between float and wall varies with the position of the float. Acceleration of the fluid through the annulus produces a pressure differential across the position of the float and an upward force on it. At the equilibrium position, which may be stabilized by a slow rotation of the float, this upward force is balanced by the weight force acting on the float. If the equilibrium is disturbed by increasing the flow rate, the balance of weight force and the pressure differential are produced by movement of the float upward to a position at which the area of the annulus is bigger. For accurate measurement, the rotameter is calibrated with the fluid to be metered. Its use is, however, restricted to that fluid.