Flow of Fluids Through Packed Beds

FLOW OF FLUIDS THROUGH PACKED BEDS

Fluid flow analysis through a permeable bed of solids is widely applied in filtration, leaching, and several other processes. A first approach may be made by assuming that the interstices of the bed correspond to a large number of discrete, parallel capillaries. If the flow is streamline, the volumetric flow rate, Q, is given for a single capillary by equation (2.14),

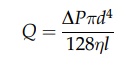
where l is the length of the capillary, d, its diameter, ΔP is the pressure drop across the capillary, and η is the viscosity of the fluid. The length of the capillary exceeds the depth of the bed of an amount that depends on its tortuosity. The depth of bed, L, is, however, proportional to the capillary length, l, so

where k is a constant for a particular bed. If the area of the bed is A and it contains n capillaries per unit area, the total flow rate is given by

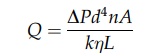
Both n and d are not normally known. However, they have certain values for a given bed, so

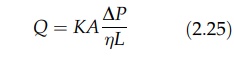
where K = d⁴n/k. This constant is a permeability coefficient, and 1/K is the specific resistance. Its value characterizes a particular bed.

The postulate of discrete capillaries precludes valid comment on the fac-tors that determine the permeability coefficient. Channels are not discrete but are interconnected in a random manner. Nevertheless, the resistance to the passage of fluid must depend on the number and dimensions of the channels. These quantities can be expressed in terms of the fraction of the bed that is void—that is, the porosity—and the manner in which the void fraction is distributed. With reference to a specific example, water would flow more easily through a bed with a porosity of 40% than through a bed of the same material with a porosity of 25%. It would also flow more quickly through a bed of coarse particles than through a bed of fine particles packed to the void fraction or porosity. The latter effect can be expressed in terms of the surface area offered to the fluid by the bed. This property is inversely proportional to the size of the particles forming the bed. Permeability increases as the porosity increases and the total surface of the bed decreases, and these factors may be combined to give the hydraulic diameter, d⁰, of an equivalent channel, defined by

d⁰ = Volume of voids / Total surface of material forming bed

The volume of voids is the porosity, and the volume of solids is 1 - ε. If the specific surface area, that is, the surface area of unit volume of solids, is S₀, the total surface presented by unit volume of the bed is S₀(1 - ε). Therefore,

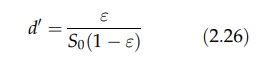
Under laminar flow conditions, the rate at which a fluid flows through this equivalent channel is given by equation (2.14) as

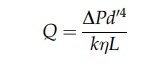
The velocity, u^’, in the channel is derived by dividing the volumetric flow rate by the area of the channel, k^’d^’2. Combining the constants produces,

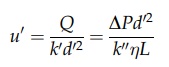
This velocity, when averaged over the entire area of the bed, solids, and voids, gives the lower value, u. These velocities are related by the equation u = u^’e. Therefore,

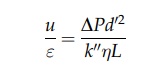
Substituting for d^’ by means of equation (2.26) gives

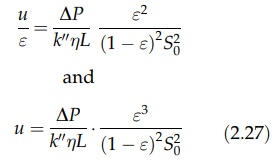
In this equation, known after its originator as Kozeny’s equation, the constant  k’  has a value of 5 ± 0.5. Since Q = uA, where A is the area of the bed, equation (2.27) can be transformed to

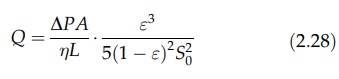
This analysis shows that permeability is a complex function of porosity and surface area, the latter being determined by the size distribution and shape of the particles. The appearance of specific surface in equation (2.28) offers a method for its measurement and provides the basis of fluid permeation methods of size analysis. This equation also applies to the studies of filtration.