Exchange of Radiation

EXCHANGE OF RADIATION

The exchange of radiation is based on two laws. The first, known as Kirchhoff’s law, states that the ratio of the emissive power to the absorptivity is the same for all bodies in thermal equilibrium. The emissive power of a body, E, is the radiant energy emitted from unit area in unit time (J/m² sec). A body of area A₁ and emissivity E₁, therefore, emits energy at a rate E₁A₁. If the radiation falling on unit area of the body is E_b, the rate of energy absorption is E_ba₁A₁, where a₁ is the absorptivity. At thermal equilibrium, E_ba₁A₁ = E₁A. For another body in the same environment, E_ba₂A₂ = E₂A₂. Therefore,

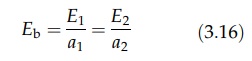
For a blackbody, a = 1. The emissive power is therefore E_b. The blackbody is a perfect radiator, and it is used as the comparative standard for other sur-faces. The emissivity of a surface is defined as the ratio of the emissive power, E, of the surface to the emissive power of a blackbody at the same temperature, E_b.

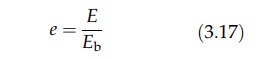
The emissivity is numerically equal to the absorptivity. Since the emissive power varies with wavelength, the ratio should be quoted at a particular wavelength. For many materials, however, the emissive power is a constant fraction of the blackbody radiation, that is, the emissivity is constant. These materials are known as gray bodies.

The second fundamental law of radiation, known as the Stefan Boltzmann law, states that the rate of energy emission from a blackbody is proportional to the fourth power of the absolute temperature, T.

E= σT⁴                         (3:18)

where E is the total emissive power and σ is the Stefan Boltzmann constant, the numerical value of which is 5.676 x 10^-8 J/m²·sec·K⁴. It is sufficiently accurate to say that the heat emitted in unit time, Q, from a blackbody of area A is given by

Q = σAT⁴

and for a body that is not perfectly black by

Q = σeAT⁴                   (3:19)

where e is the emissivity.

The net energy gained or lost by a body can be estimated with these laws. The simplest case is that of a gray body in black surroundings. These conditions, in which none of the energy emitted by the body is reflected back, are approximately those of a body radiating to atmosphere. If the absolute tem-perature of the body is T₁, the rate of heat loss is σeAT₁⁴ [equation (3.19)], where A is the area of the body and e is its emissivity. Surroundings at a temperature T₂ will emit radiation proportional to σT₂⁴, and a fraction, determined by area and absorptivity, a, will be absorbed by the body. This heat will be σaAT₂⁴, and since absorptivity and emissivity are equal,

Net heat transfer rate = σeA(T₁⁴ - T₂⁴)                      (3:20)

If part of the energy emitted by a surface is reflected back by another surface, the calculation of radiation exchange is more complex. Equations for various surface configurations are available. These take the general form

Q = F₁F₂σA(T_A⁴ - T_B⁴)

where F₁ and F₂ are factors determined by the configuration and emissivity of surfaces at temperatures T_A and T_B.

Example Problems

Example 1

A stainless steel pipe has an internal radius of 0.019 m and an external radius of 0.024 m. The thermal conductivity of stainless steel is 34.606 J/m·sec·K. Steam at 422 K surrounds the pipe that is lagged with 0.051 m of insulation with a conductivity of 0.069 J/m·sec·K. The temperature of the outer surface of the insulation is 311 K. What is the heat loss per meter of pipe? For the wall of the pipe,

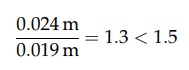
Therefore, the arithmetic mean best defines the radius.

Therefore, the logarithmic mean best defines the radius.

For the insulation,

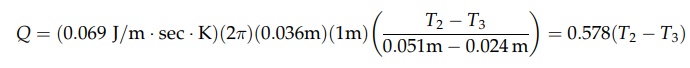
Rearranging these equations gives the following:

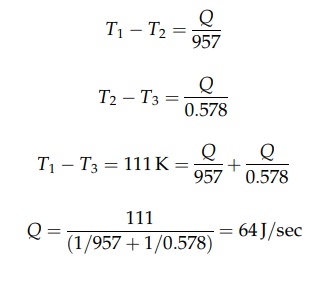
Example 2

A 0.051-m uninsulated horizontal pipe is carrying steam at 389 K to the surroundings at 294 K. The emissivity, e, of the pipe is 0.8. Absolute zero is 273 K.

Find the heat loss by radiation.

Heat loss / Unit length = (5:676 10^-8 J=m² sec K⁴)(0:058 m)(π)(0:8)[(116K)⁴ - 21K)⁴]

 = 1.50 J/m sec