Equimolecular Counter Diffusion

EQUIMOLECULAR COUNTERDIFFUSION

If no bulk flow occurs in the element of length dx, shown in Figure 4.1, the rates of diffusion of the two gases, A and B, must be equal and opposite, that is,

N_A= - N_B

The partial pressure of A changes by dP_A over the distance dx. Similarly, the partial pressure of B changes by dP_B. Since there is no difference in total pressure across the element (no bulk flow), dP_A/dx must equal -dP_B/dx. For an ideal gas, the partial pressure is related to the molar concentration by the relation

P_AV = n_ART

where n_A is the number of moles of gas A in a volume V. Since the molar concentration, C_A, is equal to n_A/V,

P_A = C_ART

Therefore, for gas A, equation (4.1) can be written as

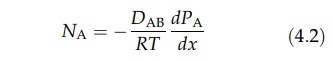
where D_AB is the diffusivity of A in B. Similarly,

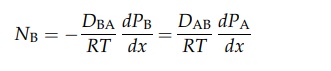
It therefore follows that D_AB = D_BA = D. If the partial pressure of A at x₁ is P_A1 and that at x₂ is P_A2, integration of equation (4.2) gives

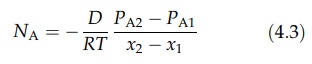
A similar equation may be derived for the counterdiffusion of gas B.