Mass Transfer in Turbulent and Laminar Flow

MASS TRANSFER IN TURBULENT AND LAMINAR FLOW

As already explained, movement of molecules across the streamlines of a fluid in laminar flow can only occur by molecular diffusion. If the concentration of a component, A, varies in a direction normal to the streamlines, the molar rate of diffusion will be given by equation (4.1).

When a fluid flows over a surface, the surface retards the adjacent fluid region, forming a boundary layer. If flow throughout the fluid is laminar, the equation for molecular diffusion may be used to evaluate the mass transferred across the boundary layer. In most important cases, however, flow in the bulk of the fluid is turbulent. The boundary layer is then considered to consist of three distinct flow regimes. In the region of the boundary layer most distant from the surface, flow is turbulent and mass transfer is the result of the interchange of large portions of the fluid. Mass interchange is rapid, and concentration gra-dients are low. As the surface is approached, a transition from turbulent to laminar flow occurs in the transition or buffer region. In this region, mass transfer by eddy diffusion and molecular diffusion are of comparable magnitude. In a fluid layer at the surface, a fraction of a millimeter thick, laminar flow conditions persist. This laminar sublayer, in which transfer occurs by molecular diffusion only, offers the main resistance to mass transfer, as shown in Figure 4.2.

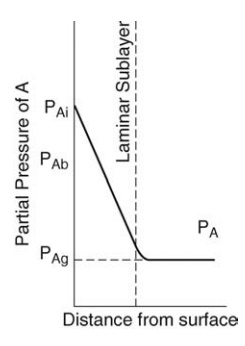
FIGURE 4.2 Mass transfer at a boundary.

As flow becomes more turbulent, the thickness of the laminar sublayer and its resistance to mass transfer decrease.

One approach to the evaluation of the rate of mass transfer under these conditions lies in the postulation of a film, the thickness of which offers the same resistance to mass transfer as the combined laminar, buffer, and turbulent regions. The analogy with heat transfer by conduction and convection is exact, and quantitative relations between heat and mass transfer can be developed for some situations. This, however, is not attempted in this text. The postulate of an effective film is explained by reference to Figure 4.2.

A gas flows over a surface, and equimolecular counterdiffusion of com-ponents A and B occurs, A away from the surface and B toward the surface. The variation in partial pressure of A with distance from the surface is shown in the figure. At the surface, the value is P_Ai. A linear fall to P_Ab occurs over the laminar sublayer. Beyond this, the partial pressure falls less steeply to the value P_A at the edge of the boundary layer. P_Ag, a value slightly higher than this, is the average partial pressure of A in the entire system. In general, the gas content of the laminar layer is so small that P_A and P_Ag are virtually equal. If molecular diffusion were solely responsible for diffusion, the partial pressure, P_Ag, would be reached at some fictitious distance, x⁰, from the surface, over which the concentration gradient (P_Ai – P_Ag)/x^’ exists. The molar rate of mass transfer would then be

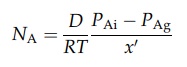
x^' is not known, however, and this equation may be written as

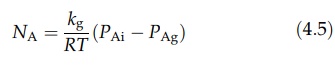
where k_g, is a mass transfer coefficient, the unit of which is m/sec. Since C_A = P_A/RT, we can also write

N_A = k_g(C_Ai - C_Ag)

where C_Ai and C_Ag are the gas concentrations at either side of the film. Similar equations describe the diffusion of B in the opposite direction.

Diffusion across a liquid film is described by the equation

N_A = k₁(C_Ai C_Al)                             (4:6)

where C_Ai is the concentration of component A at the interface and C_Al is its concentration in the bulk of the phase.

In all cases, the mass transfer coefficient will depend on the diffusivity of the transferred material and the thickness of the effective film. The latter is largely determined by the Reynolds number of the moving fluid, that is, its average velocity, its density, its viscosity, and some linear dimension of the system. Dimensional analysis will give the following relation:

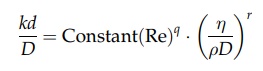
where Re is the Reynolds number, k is the mass transfer coefficient, D is the diffusivity, and d is a dimension characterizing the geometry of the system.

This relation is analogous to the expression for heat transfer by forced convection given in chapter 3. The dimensionless group kd/D corresponds to the Nusselt group in heat transfer. The parameter η/ρD is known as the Schmidt number and is the mass transfer counterpart of the Prandtl number. For example, the evaporation of a thin liquid film at the wall of a pipe into a turbulent gas is described by the equation

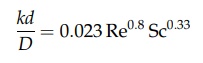
where Sc is the Schmidt number. Although the equation expresses experimental data, comparison with equation (13) from the heat transfer section again dem-onstrates the fundamental relation of heat and mass transfer.

Similar relations have been developed empirically for other situations. The flow of gases normal to and parallel to liquid surfaces can be applied to drying processes, and the agitation of solids in liquids can provide information for crystallization or dissolution. The final correlation allows the estimation of the mass transfer coefficient with reasonable accuracy.