Packing of Powders

PACKING OF POWDERS

Bulk density, already defined, and porosity are terms used to describe the degree of consolidation in a powder. The porosity, ε, is the fraction of the total volume that is void, often expressed as a percentage. It is related to the bulk density, ρ_b, by the equation

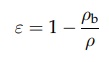
ε = 1  -  ρ_b/ρ                  (5.1)

where ρ is the true density of the powder.

When spheres of equal size are packed in a regular manner, the porosity can vary from a maximum of 46% for a cubical arrangement to a minimum of 26% for a rhombohedral array. These extremes are shown in Figure 5.4. For ideal systems of this type, the porosity is not dependent on the particle size. In practice, of course, packing is not regular. Cubic packing, obtained when the next layer is placed directly on top of the four spheres above, is the most open

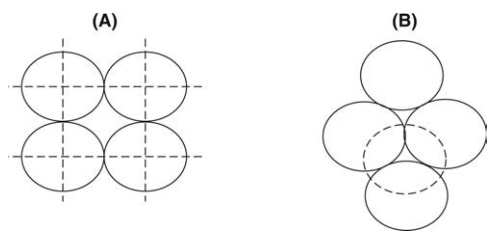
FIGURE 5.4 Systematic packing of spheres (A) open (cubic) and; (B) closed (rhombohedral) structure.

packing, as shown in Figure 5.4A. Rhombohedral packing, obtained when the next layer is built around the sphere shown in a broken line in Figure 5.4B, is the closest packing.

Nevertheless, for coarse, isodiametric particles with a narrow range of sizes, the porosity is remarkably constant at between 37% and 40%. Lead shot, for example, packs with the same porosity as a closely graded sand. With wider size distributions, the porosity decreases because some packing of fine particles in the interstices between the coarsest particles becomes possible. These effects are absent in fine powders. Because of their more cohesive nature, the porosity increases as the particles become finer and variation in the size distribution has little effect.

In any irregular array, the porosity increases as particle shape departs from sphericity because open packing and bridging become more common. A flaky material, such as crushed mica, packs with a porosity of about 90%. Roughness of the surface of the particles will increase porosity.

In operations in which powders are poured, chance packing occurs and the porosity is subject to the speed of the operation and the degree of agitation. If the powder is poured slowly, each particle can find a stable position in the developing surface. Interstitial volumes will be small, the number of contacts with neighboring particles will be high, and the porosity will be low. If pouring is quick, there is insufficient time for stable packing, bridges are created as particles fall together, and a bed of higher porosity is formed. Vibration opposes open packing and the formation of bridges. It is often deliberately applied when closely packed powder beds are required.

Packing at a boundary differs from packing in the bulk of a powder. The boundary normally creates a region of more open packing, several particle layers in extent. This is important when particles are packed into small vol-umes. If the particles are relatively large, the region of expanded packing and low bulk density will be extensive, and for these conditions, the weight of material that fills the volume will decrease as the particle size increases. With finer powders, the opposite is true and cohesiveness causes the weight of powder that fills a volume to decrease as the particle size decreases. There is, therefore, some size of particle for which the capacity of a small volume is a maximum. This depends on the dimensions of the space into which the par-ticles are packed.