Mass Spectrometry

MASS SPECTROMETRY

Mass spectrometry is not a true spectroscopic technique that involves absorption of energy at particular frequencies. Rather one excites the molecule as a whole and then observes its subsequent reactions. The use of MS for structure deter-mination might be described as chemical archeology. A real archaeologist picks up fragments of a pot or other vessel, identifies them, fits them back together, and can tell what the original object was in great detail. In MS a molecule is purposely broken into pieces, the pieces are identified by mass, and the original structure is then inferred from the pieces.

To measure the mass spectrum, a molecule is bombarded with a stream of energetic electrons (70 eV) and one of the electrons of the molecule is ejected from one of the orbitals after a collision.

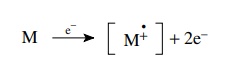
This produces a charged species with an unpaired electron called a radical cation. The first formed radical cation is called the molecular ion because it contains all of the atoms present in the starting molecule. The molecular ion contains a large amount of excess energy deposited by the collision which dislodged the electron. Considering that electrons of 70 eV energy contain 1613.5 kcal/mol energy, the molecular ion usually contains energies far in excess of bond dissociation energies (80 – 100 kcal/mol) so it dissociates into fragments.

Fragmentation processes must conserve both charge and spin; thus a radical cation can undergo the following types of cleavages. The fragment products also contain excess energy since fragmentations are adiabatic, and they can themselves undergo further fragmentations to smaller pieces.

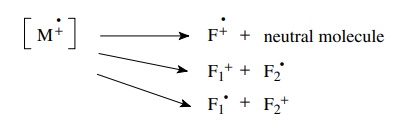
Generally fragmentations occur very rapidly in the region where the initial ionization takes place called the source. The packet of ions, which includes the molecular ion and the fragment ions, is then accelerated by an electric field, focused through slits, and the beam of ions travels at high speed down a curved tube toward the detector. At this point one can think of the ion beam as a stream of charged projectiles having different masses. Now moving charges are subject to the influences of electric and/or magnetic fields so if a magnetic field (or electric field) is applied to the ion beam, the path of the particles will curve. When the trajectory of a particle matches the curve of the tube, the particle will reach the detector. If not, it will hit the wall and be annihilated (Figure 11.43).

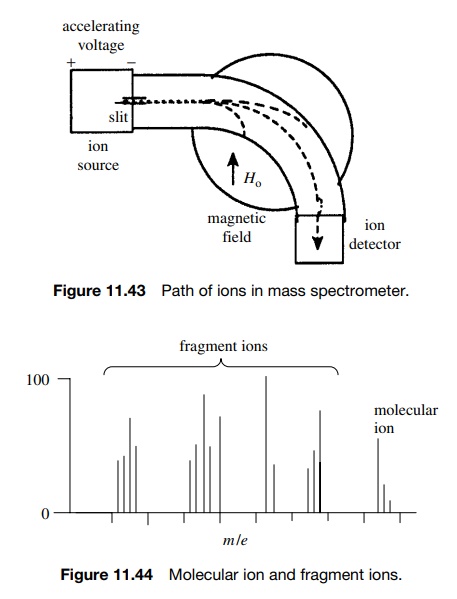
The path of the moving ion will curve according to its speed, mass-to-charge ratio (m/e), and the strength of the electric or magnetic field through which it passes. Fragments of low m/e will curve more than fragments of higher m/e. Thus if the ion packet is accelerated uniformly, the magnetic or electric field can be varied so that fragments of different m/e values can be curved to strike the detector and counted in turn. 

What results are a series of signals corresponding to different m/e values for the various charged fragments produced from the molecular ion (Figure 11.44).

The vast majority of fragments will have only a single positive charge (i.e., e = 1); thus the m/e of a given ion corresponds to the mass of the ion in atomic mass units. It is very important to remember that only ions (cations or radical cations) are detected — neutral species (closed-shell molecules or radicals) are not detected because they are not accelerated and they are not influenced by the applied field. Thus MS yields information about the mass of the molecular ion and the masses of fragment ions produced from the molecular ion. This so-called cracking pattern provides information about connectivity in the molecule that can be used to reconstruct the intact precursor molecule.

The molecular ion is one of the most important ions in the mass spectrum of a compound for the following reasons:

1. The m/e value of the molecular ion is equal to the molecular weight (MW) of the compound. This gives a rough estimate of the number of carbon atoms. Furthermore a knowledge of the history of the sample and the reagents used often permits the molecular formula to be deduced.

For example, treatment of p-toluic acid with ethyl iodide and potassium carbonate gave an oil whose molecular ion is at m/e = 164. This molecular ion corresponds to the addition of 28 mass units to the starting material, consistent with the formation of an ethyl ester by displacement of iodide.

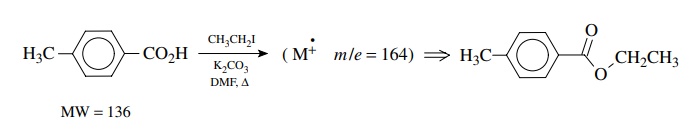
2. High-resolution mass spectrometers which can measure m/e values to four decimal places are capable of confirming the molecular formula of the molecular ions. These so-called exact mass measurements can be used because the atomic weights of the elements are not exactly whole numbers (except for ¹²C, which is the standard at 12.0000 amu). The exact masses of some elements and their most abundant isotopes are given in Table 11.2. To find the exact mass of a molecule, the atomic mass of the most abundant isotope for each element is used to calculate the exact mass of the com-pound. This is compared to the exact mass measured on a high-resolution mass spectrometer. If the two values agree to the third decimal point, then it is certain that the molecular formula used to calculate the exact mass is correct.

Consider the three compounds C₈H₁₆N₂, C₉H₁₈N, C₉H₁₆O. All would give a molecular ion of m/e = 140 in the low-resolution mass spectrum. Using the elemental exact masses in Table 11.2, the molecular exact masses are calculated:

C₈H₁₆N₂ ⇒ (8 × 12.000) + (16 × 1.00783) + (2 × 14.0031) = 140.13148

C₉H₁₈N ⇒ (9 × 12.000) + (18 × 1.00783) + (14.0031) = 140.14404

C₉H₁₆O = (9 × 12.000) + (16 × 1.00783) + 15.9949 = 140.12018

It is clear that if the mass of the molecular ion can be determined to 0.001 amu, these three compounds can be distinguished clearly. Instead of having to calculate exact masses, there are many published tables of exact masses for any elemental composition and there are many computer programs that calculate the exact mass after input of the molecule formula.

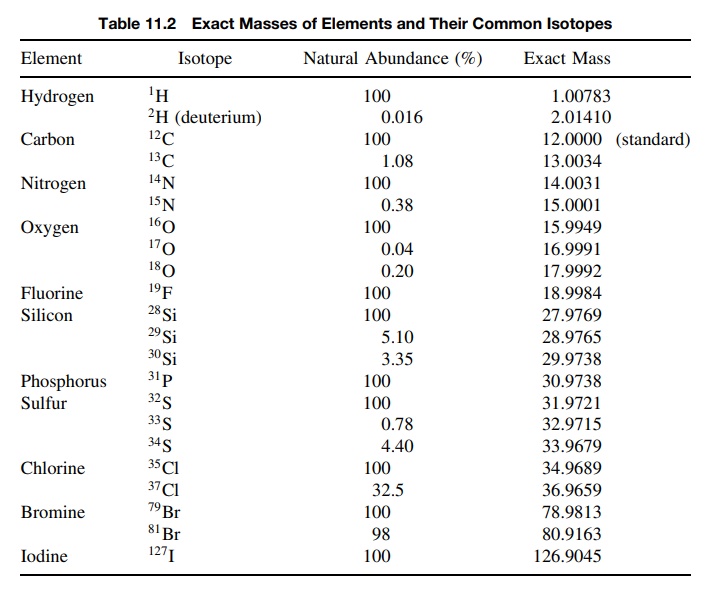
3. The analysis of isotopic clusters of the molecular ion can be used to infer the presence of elements based on their isotopes. The molecular ion cor-responds to the m/e for the ion corresponding to some molecular formula. Examination of the molecular ion (Figure 11.45) reveals that in addition to the expected molecular ion, there is normally a smaller peak at M + 1 and an even smaller one at M + 2. These are due to the fact that there are naturally occurring isotopes of higher mass that, if present in a given molecule, cause its mass to be higher than for the lighter isotopes.

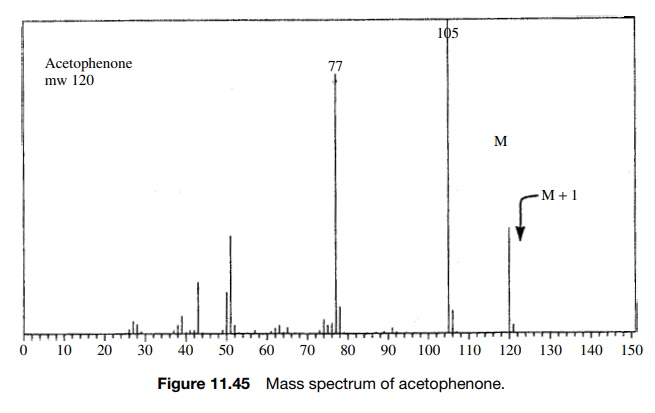
The most obvious example of such behavior is for molecules which contain chlorine or bromine. The two isotopes of chlorine occur naturally in the ratio of ³⁵Cl : ³⁷Cl = 100 : 32.7 (3.058 : 1). 

A molecule such as chlorobenzene would exhibit two distinct molecular ions— one at m/e = 112 for those molecules which have the ³⁵Cl isotope and one at m/e = 114 for those molecules which con-tain the ³⁷Cl isotope. The intensities of these peaks should be 3.058 : 1, reflecting the probability that a molecule has one or the other of the isotopes (Figure 11.46).

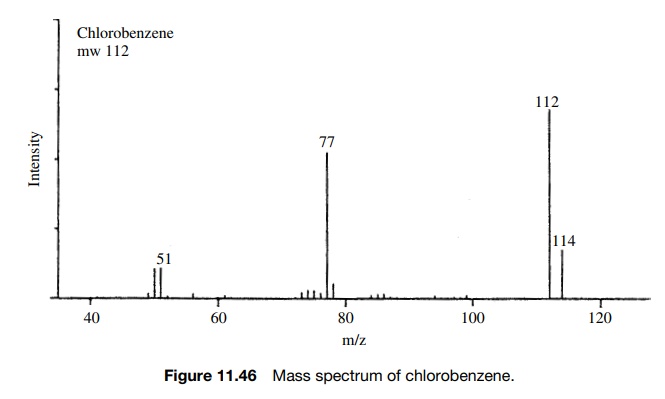
A similar situation is seen for molecules containing bromine. The isotopes ⁷⁹Br and ⁸¹Br occur in a ratio ⁷⁹Br/⁸¹Br = 100 : 97.5 (1.026 : 1). Thus a molecule such as ethyl bromoacetate will exhibit molecular ions at m/e = 166 and m/e = 168 for molecules which contain ⁷⁹Br and ⁸¹Br, respectively. The ratio of peak intensities will be 1.026 : 1 because this is the relative abundance of the two bromine isotopes present in the molecule (Figure 11.47).

Now if a molecule contains more than one chlorine atom, the appearance of isotope clusters can be calculated by the probabilities of isotope distributions and the natural abundances of the isotopes. For example, if a molecule contains two chlorine atoms such as o-dichlorobenzene, then there will be peaks at M, M + 2, and M + 4 for molecules which have two ³⁵Cl, one ³⁵Cl and one ³⁷Cl, and two ³⁷Cl (Figure 11.48).

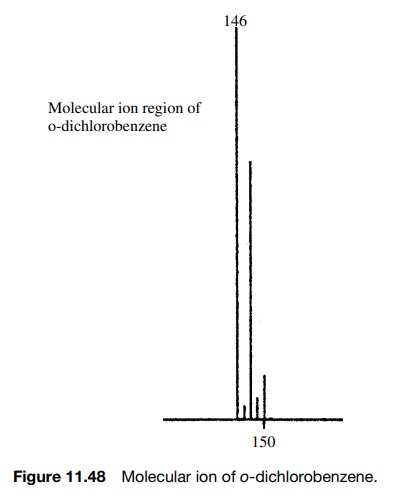
The relative intensities of these peaks can be calculated by taking into account the number of combinations that can give the required isotopic substitution and the probability of an isotope being present. An M + 2 peak in the above example will result if either of the chlorine atoms is ³⁷Cl; thus the intensity of an M + 2 peak will be 2 × (1/3.058). An M + 4 peak will occur only if both chlorine atoms are ³⁷Cl; thus the intensity of the M + 4 peak will be 2 × (1/3.058)². The squared term follows from the necessity that both chlorine atoms must be ³⁷Cl. Thus the intensities of the peaks in the isotopic cluster of the molecular ion are (approximately) given as

M : M+2:M+4=1:(2× 1/3):1×(1/3)² =1:0.66:0.111

The presence of isotopic clusters is particularly clear for molecules containing chlorine or bromine because of the abundance of two isotopes. The same consid-erations are applicable, however, for other elements that have smaller abundances of higher isotopes. These natural isotopic abundances are given in Table 11.2. As can be seen, ¹³C is present to the extent of 1.08% of ¹²C while ²H is present only to the extent of .016% of ¹H. Now if a molecule such as benzene is examined, the molecular ion is found at m/e = 78 but there are an M + 1 peak and an M + 2 peak whose intensities are 6.58% and 0.22%. The M + 1 peak is due to the probability that one of the six carbons will be ¹³C or one of the six hydrogens will be deuterium. The M + 2 peak is due the probability that two of the carbons in the same molecule will be ¹³C (the probability of two deuterium atoms in the same molecule is exceedingly small) or that one ¹³C and one deuterium are present in the same molecule. The intensities of M + 1 and M + 2 peaks can be calculated for various molecular formulas based on these probabilities and they have been tabulated in several texts.

This information can be used to deduce the elemental composition of a com-pound. For example, the oxidation of 1,2-diazacyclohexane was carried out in cyclohexane. A product was isolated and was found to have a molecular ion of m/e = 84. At this point the experimenter realized that both the expected product and the reaction solvent have a molecular weight of 84.

Measurement of the isotopic cluster of the molecular ion showed an M + 1 peak of 5.30% and an M + 2 peak of 0.15% of the molecular ion. From tables of isotopic abundance ratios it was found that the expected product C₄H₈N₂ should give M + 1 and M + 2 peaks of 5.21 and 0.11%, respectively, while cyclohexane C₆H ₁₂ should give M + 1 and M + 2 peaks of 6.68 and 0.19%, respectively. It is clear that the isolated product is most likely the expected cyclic azo compound and not cyclohexane.

Of course nowadays exact mass measurement could also distinguish these two molecules, as could a variety of other instrumental techniques. The analysis of isotopic clusters is most useful for detecting the presence of halogens, sulfur, and silicon, all of which have abundant isotopes of two atomic weight units higher, thus leading to relatively large M + 2 peaks.