Paired t Test

PAIRED t TEST

Previously, we covered statistical tests (e.g., the independent groups Z test and t test) for assessing differences between group means derived from independent sam-ples. In some medical applications, we use measures that are paired; examples are comparison of pre–post test results from the same subject, comparisons of twins, and comparisons of littermates. In these situations, there is an expected correlation (relationship) between any pair of responses. The paired t test looks at treatment differences in medical studies that have paired observations.

The paired t test is used to detect treatment differences when measurements from one group of subjects are correlated with measurements from another. You will learn about correlation in more detail in Chapter 12. For now, just think of correla-tion as a positive relationship. The paired t test evaluates within-subject compar-isons, meaning that a subject’s scores collected at an earlier time are compared with his own scores collected at a later time. The scores of twin pairs are analogous to within-subject comparisons.

The results of subjects’ responses to pre- and posttest measures tend to be relat-ed. To illustrate, if we measure children’s gains in intelligence over time, their later scores are related to their initial scores. (Smart children will continue to be smart when they are remeasured.) When such a correlation exists, the pairing can lead to a mean difference that has less variability than would occur had the groups been com-pletely independent of each other. This reduction in variance implies that a more powerful test (the paired t test) can be constructed than for the independent case. Similarly, paired t tests can allow the construction of more precise confidence inter-vals than would be obtained by using independent groups t tests.

For the paired t test, the sample sizes n_t and n_c must be equal, which is one disad-vantage of the test. Paired tests often occur in crossover clinical trials. In such trials, the patient is given one treatment for a time, the outcome of the treatment is mea-sured, and then the patient is put on another treatment (the control treatment). Usu-ally, there is a waiting period, called a washout period, between the treatments to make sure that the effect of the first treatment is no longer present when the second treatment is started.

First, we will provide background information about the logic of the paired t test and then give some calculation examples using the data from Tables 9.1 and 9.2. Matching or pairing of subjects is done by patient; i.e., the difference is taken be-tween the first treatment for patient A and the second treatment for patient A, and so on for patient B and all other patients. The differences are then averaged over the set of n patients.

As implied at the beginning of this section, we do not compute differences be-tween treatment 1 for patient A and treatment 2 for patient B. The positive correla tion between the treatments exists because the patient himself is the common factor. We wish to avoid mixing patient-to-patient variability with the treatment effect in the computed paired difference. As physicians enjoy saying, “the patient acts as his own control.”

Order effects refer to the order of the presentation of the treatments in experi-mental studies such as clinical trials. Some clinical trials have multiple treatments; others have a treatment condition and a control or placebo condition. Order effects may influence the outcome of a clinical trial. In the case in which a patient serves as his own control, we may not think that it matters whether the treatment or con-trol condition occurs first. Although we cannot rule out order effects, they are easy to minimize; we can minimize them by randomizing the order of presentation of the experimental conditions. For example, in a clinical trial that has a treatment and a control condition, patients could be randomized to either leg of the trial so that one-half of the patients would receive the treatment first and one-half the control first.

By looking at paired differences (i.e., differences between treatments A and B for each patient), we gain precision by having less variability in these paired differences than with an independent-groups model; however, the act of pairing discards the individual observations (there were 2n of them and now we are left with only n paired differences). We will see that the resulting t statistic will have only n – 1 degrees of freedom rather than the 2n – 2 degrees of freedom as in the t test for differences between means of two independent samples.

Although we have achieved less variability in the sample differences, the paired t test cuts the sample size by a factor of two. When the correlation between treatments A and B is high (and consequently the variability is reduced considerably), pairing will pay off for us. But if the observations being paired were truly independent, the pairing could actually weaken our analysis.

A paired t-test (two-sided test) consists of the following steps:

1. Form the paired differences.

2. State the null hypothesis H₀: μ_t = μ_c versus the alternative hypothesis H₁: μ_t ≠ μ_c. (As H₀: μ_t = μ_c, we also can say H₀: μ_t – μ_c = 0; H₁: μ_t – μ_c ≠ 0.)

3. Choose a significance level α = α₀ (often we take α₀ = 0.05 or 0.01).

4. Determine the critical region; that is, the region of values of t in the upper and lower α/2 tails of the sampling distribution for Student’s t distribution with n - 1 degrees of freedom when μ_t/μ_c (i.e., the sampling distribution when the null hypothesis is true) and when n = n_t = n_c.

5. Compute the t statistic: t = 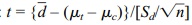 for the given sample and sample size n for the paired differences, where ^–d^- is the sample mean differ-ence between groups and s_d is the sample standard deviation for the paired differences.

6. Reject the null hypothesis if the test statistic t (computed in step 4) falls in the rejection region for this test; otherwise, do not reject the null hypothe-sis.

Now we will now look at an example of how to perform a paired t test. A striking example where the correlation between two groups is due to a seasonal effect follows. Although it is a weather example, these kinds of results can occur easily in clinical trial data as well. The data are fictitious but are realistic temperatures for the two cities at various times during the year. We are considering two temperature readings from stations that are located in neighboring cities such as Washington, D.C., and New York. We may think that it tends to be a little warmer in Washing-ton, but seasonal effects could mask a slight difference of a few degrees.

We want to test the null hypothesis that the average daily temperatures of the two cities are the same. We will test this hypothesis versus the two-sided alternative that there is a difference between the cities. We are given the data in Table 9.1, which shows the mean temperature on the 15th of each month during a 12-month period.

Now let us consider the two-sample t test as though the data for the cities were independent. Later we will see that this is a faulty assumption. The means for Washington (₁) and New York (₂) equal 56.16°F and 52.5°F, respectively. Is the difference (3.66) between these means statistically significant? We test H₀: μ₁ – μ₂ = 0 against the alternative H₁: μ₁ – μ₂ ≠ 0, where μ₁ is the population mean temperature for Washington and μ₂ is the population mean temperature for New York. The respective sample standard deviations, S₁ and S₂, equal 23.85 and 23.56. These sample standard deviations are close enough to make plausible the assumption that the population standard deviations are equal.

Consequently, we use the pooled variance S_p² = {S²₁(n₁ – 1) + S²₂(n₂–1)}/[n₁ + n₂ - 2]. In this case, S_p² = [11(23.85)² + 11 (23.56)²]/22. These data yield S_p² = 561.95 or S_p = 23.71. Now the two-sample t statistic is t = (56.16 – 52.5)/ √{561.95(2/12)} = 3.66/ √{561.95/6} = 3.66/9.68 = 0.378. Clearly, t = 0.378 is not significant. From the table for the t distribution with 22 degrees of freedom, the critical value even for α  = 0.10 would be 1.7171. So it seems to be convincing that the difference is not significant.

TABLE 9.1. Daily Temperatures in Washington and New York

But let us look more closely at the data. The independence assumption does not hold. We can see that temperatures are much higher in summer months than in win-ter months for both cities. We see that the month-to-month variability is large and dominant over the variability between cities for any given day. So if we pair tem-peratures on the same days for these cities we will remove the effect of month-to-month variability and have a better chance to detect a difference between cities. Now let us follow the paired t test procedure based on data from Table 9.2.

Here we see that the mean difference  is again 3.66 but the standard deviation S_d = 1.614, which is a dramatic reduction in variation over the pooled estimate of 23.71! (You can verify these numbers on your own by using the data from Table 9.2.)

We are beginning to see the usefulness of pairing: t = ( – (μ₁ – μ₂))/(S_d/√n) = (3.66 – 0)/(1.614/√12) = 3.66/0.466 = 7.86. This t value is highly significant be-cause even for an alpha of 0.001 with a t of 11 degrees of freedom (n –1 = 11), the critical value is only 4.437!

This outcome is truly astonishing! Using an unpaired test with this temperature data we were not even close to a statistically significant result, but with an appropri-ate choice for pairing, the significance of the paired differences between the cities is extremely high. These two opposite findings indicate how wrong one can be when using erroneous assumptions.

There is no magic to statistical methods. Bad assumptions lead to bad answers. Another indication that it was warmer in Washington than in New York is the fact that the average temperature in Washington was higher for all twelve days.

In Section 14.4, we will consider a nonparametric technique called the sign test. Under the null hypothesis that the two cities have the same mean temperatures each day of the year, the probability of Washington being warmer than New York would be 0.5 on each day. In the sample, this outcome occurs 12 days in a row. According to the sign test, the probability of this outcome under the null hypothesis is (0.50)12 = 0.00024.

TABLE 9.2. Daily Temperatures for Two Cities and Their Paired Differences

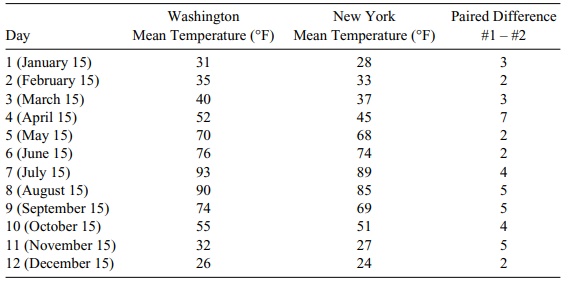
Finally, let us go through the six steps for the paired t test using the temperature data:

1. Form the paired differences (the far right column in Table 9.2).

2. State the null hypothesis H₀: μ₁ = μ₂ or μ₁ – μ₂ = 0 versus the alternative hypothesis H₁: μ₁ ≠ μ₂ or μ₁ – μ₂ ≠ 0.

3. Choose a significance level α = α₀ = 0.01.

4. Determine the critical region, that is, the region of values of t in the upper and lower 0.005 tails of the sampling distribution for Student’s t distribution with n – 1 = 11 degrees of freedom when μ₁ = μ₂ (i.e., the sampling distribution when the null hypothesis is true) and when n = n₁ = n₂.

5. Compute the t statistic: t = { – (μ₁ – μ₂)}/[S_d/√n] for the given sample and sample size n for the paired differences, where d = 3.66 is the sample mean difference between groups and S_d = 1.614 is the sample standard deviation for the paired differences.

6. Reject the null hypothesis if the test statistic t (computed in step 5) falls in the rejection region for this test; otherwise, do not reject the null hypothesis. For a t with 11 degrees of freedom and α = 0.01, the critical value is 3.1058. Be-cause the test statistic t is 7.86, we reject H₀.