Meta-Analysis

META-ANALYSIS

Two problems often occur regarding clinical trials:

1. Often, clinical studies do not encompass large enough samples of patients to reach definitive conclusions.

2. Two or more studies may have conflicting results (possibly because of type I and type II errors).

A technique that is being used more and more frequently to address these problems is meta-analysis. Meta-analyses are statistical techniques for combining data, sum-mary statistics, or p-values from various similar tests to reach stronger and more consistent conclusions about the results from clinical trials and other empirical studies than is possible with a single study.

Care is required in the selection of the trials to avoid potential biases in the process of combining results. Several excellent books address these issues, for ex-ample, Hedges and Olkin (1985). The volume edited by Stangl and Berry (2000) presents several illustrations that use the Bayesian hierarchical modeling approach. The hierarchical approach puts a Bayesian prior distribution on the unknown para-meters. This prior distribution will depend on other unknown parameters called hy-perparameters. Additional prior distributions are specified for the hyperparameters, thus establishing a hierarchy of prior distributions. It is not important for you to un-derstand the Bayesian hierarchical approach, but if you are interested in the details, see Stangl and Berry (2000). We will define prior and posterior distributions and Bayes rule in the next section. Bayesian hierarchical models are also used in an in-ferential approach called the empirical Bayes method. You might encounter this ter-minology if you study some of the literature.

In this section, we will show you two real-life examples in which Chernick used a particular method, Fisher’s test, which R. A. Fisher (1932) and K. Pearson (1933) developed for combining p-values in a meta-analysis. These illustrations will give you some appreciation of the value of meta-analysis and will provide you with a simple tool that you could use, given an appropriate selection of studies.

The rationale for Fisher’s test is as follows: The distribution theory for a test sta-tistic proposed that under the null hypothesis each study would have a p-value that comes from a uniform distribution on the interval [0, 1]. Denote a particular p-value by the random variable U. Let L also refer to a random variable. Now consider the transformation L = –2 ln(U) where ln is the logarithm to the base e. It can be shown mathematically that the random variable L has a chi-square distribution with 2 de-grees of freedom. (You will encounter a more general discussion of the chi-square distribution in Chapter 11.)

Suppose we have k independent trials to be combined and U₁, U₂, U₃, . . . , U_k are the random variables denoting the p-values for the k independent trials. Now consider the variable L_k = –2 ln(U₁, U₂, U₃, . . . , U_k) = –2 ln(U₁) – 2 ln(U₂) – 2 ln(U₃) – . . . – 2 ln(U_k); then L_k is the sum of k independent chi-square random variables each with 2 degrees of freedom. It is known that the sum of independent chi-square random variables is a chi-square random variable with degrees of free-dom equal to the sum of the degrees of freedom for the individual chi-square ran-dom variables in the summation. Therefore, L_k is a chi-square variable with 2k de-grees of freedom.

The chi-square with 2k degrees of freedom is, therefore, the reference distribu-tion that holds under the null hypothesis of no effect. We will see in the upcoming examples that the alternative of a significant difference should produce p-values that are concentrated closer to zero rather than being uniformly distributed. Lower values of the U’s lead to higher values of L_k. So we select a cutoff based on the up-per tail of the chi-square with 2k degrees of freedom. The critical value is deter-mined, of course, by the significance level that we specify for Fisher’s test.

In the first example, one of us (Chernick) was consulting for a medical device company that manufactured an instrument called a cutting balloon for use in angio-plasty procedures. The company conducted a controlled clinical trial in Europe and in the United States to show a reduction in restenosis rate for the cutting balloon an-gioplasty procedure over conventional balloon angioplasty. Other studies indicated that conventional angioplasty had a restenosis rate near 40%.

The manufacturer had seen that procedures with the cutting balloon were achiev-ing rates in the 20%–25% range. They powered the trial to detect at least a 10% im-provement (i.e., reduction in restenosis). However, results were somewhat mixed, possibly due to physicians’differing angioplasty practices and differing patient selection criteria in the various countries.

Example 8.5.2 in Chernick (1999) presents the clinical trial results using the bootstrap for a comparative country analysis. The results of the meta-analysis, not reported there, are given in Table 9.5. Countries A, B, C, and D are European coun-tries, and country E is the United States.

TABLE 9.5. Balloon Angioplasty Restenosis Rates by Country

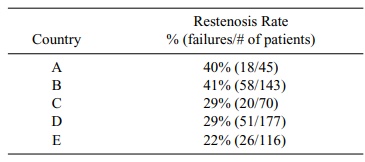
The difficulty for the manufacturer was that although the rate of 22% in the United States was statistically significantly lower than the 40% that is known for conventional balloon angioplasty, the values in countries A and B were not lower, and the combined results for all countries were not statistically significantly lower than 40%. Some additional statistical analyses gave indications about variables that ex-plained the differences. These explanations led to hypotheses about the criteria for selection of patients.

However, these data were not convincing enough for the regulatory authorities to approve the procedure without some labeling restrictions on the types of patients eligible for it. The procedure did not create any safety issues relative to convention-al angioplasty. The company was aware of several other studies that could be com-bined with this trial to provide a meta-analysis that might be more definitive. Cher-nick and associates conducted the meta-analysis using Fisher’s method for combining p-values.

In the analysis, Chernick considered six peer-reviewed studies of the cutting bal-loon along with the combined results for the clinical trial already mentioned (re-ferred to as GRT). In the latter study, sensitivity analyses also were conducted re-garding the choice of studies to include with the GRT. The other six studies are referred to by the name of the first listed author of each study. (Refer to Table 9.6.)

The variable CB ratio refers to the restenosis rate for the cutting balloon, where-as PTCA ratio is the corresponding restenosis rate for conventional balloon-angio-plasty-treated patients. Table 9.6 shows the results for these studies and the com-bined Fisher test. Here k = 7 (the number of independent trials), so the reference chi-square distribution has 14 (2k) degrees of freedom.

The table provides the individual p-values (the U’s for the Fisher chi-square test) that are based on a procedure called Fisher’s exact test for comparing two propor-tions (see Chapter 11). Note that we have two test procedures here; both are called Fisher’s test because they were devised by the same famous statistician, R. A. Fish-er. However, there is no need for confusion. Fisher’s exact test is applied in each study to compare the restenosis rates and calculate the individual p-values. Then we use these seven p-values to compute Fisher’s chi-square statistic in order to deter-mine their combined p-value. Note that the most significant test was Suzuki with a p-value of 0.001, and the least significant was the GRT itself with a p-value equal to 0.7455. However, the combined p-value is a convincing 0.000107.

TABLE 9.6. Meta-Analysis for Combined p-values in Balloon Angioplasty Studies

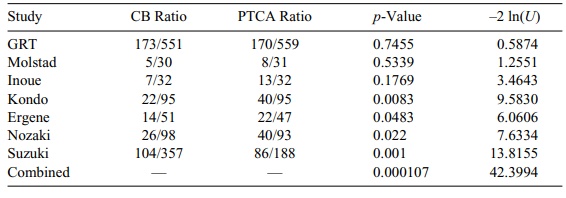
TABLE 9.7. Comparison of Blood Loss Studies with Combined Meta-Analysis

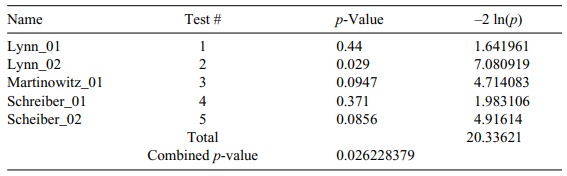
In the next example, we look at animal studies of blood loss in pigs when com-paring the use of Novo Nordisk’s clotting agent NovoSeven® with conventional treatment. Three investigators performed five studies; the results of the individual tests for mean differences and Fisher’s chi-square test are given in Table 9.7.

It is interesting to note here that although in all studies we used the Wilcoxon test for differences, it does not matter what tests are used to obtain the individual p-val-ues. All we need is that the individual p-values have a uniform distribution under the null hypothesis and be independent of the other tests. Generally, these condi-tions are met for a large variety of parametric and nonparametric tests. We could have mixed t tests with Wilcoxon or with any other test of the null hypotheses.