Sample Size Determination for Hypothesis Tests

SAMPLE SIZE DETERMINATION FOR HYPOTHESIS TESTS

In Section 8.10, we showed you how to determine the required sample size based on a criterion for confidence intervals, namely, to require the half-width or width of the confidence interval to be less than a specified δ. For hypothesis testing, one can also set up a criterion for sample size. Recall from Section 9.8 that we defined and illustrated in a particular example the power function for a two-sided test. We showed that if the level of a two-sided test (such as for a population mean or mean difference) is α, then the power of the test at the null hypothesis value (e.g., μ₀ for a population mean) is equal to α and increases as we move away from the null hypothesis value.

We learned that the power function is symmetric about the null hypothesis value and increases to 1 as we move far away from that value. We also saw that when the sample size is increased, the power function increases rapidly. This information suggests that we could specify a level of power (e.g., 90%) and a separation such that for a true mean satisfying | μ – μ₀| > δ, the power of the test at that value of μ is at least 90%.

For a given δ, this will not be achieved for small sample sizes; however, as the sample size increases there will be eventually a minimum value n at which the power will exceed 90% for the given δ. Various software packages including nQuery Advisor, PASS 2000, and Power and Precision enable you to calculate the required n  or to determine the power that can be achieved at that δ for a specified n.

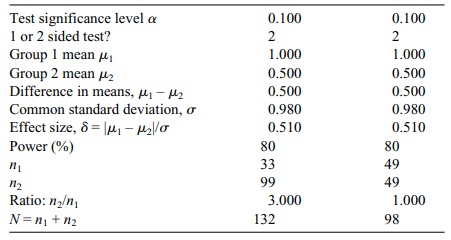
In the Tendril DX clinical trial, Chernick and associates calculated the difference between the treatment and control group means using an unpaired t test; the sample size was n_t = 3n_c, where n_t was the sample size for the treatment group and n_c was the sample size for the control group. In this problem, Chernick took δ = 0.5 volts, set the power at 80%, and assumed a common σ tested at the 0.10 significance level for a two-sided test. The resulting calculations required a sample size of 99 for the treatment group and 33 for the control group, leading to a total sample size of 132. Note that if instead we required n_t = n_c, then the required value for n_t is 49 for a total sample size of 98. Table 9.3 shows the actual table output from nQuery. In most cases, you can rely on the software to give you the solution. In some cases, there is not a simple formula, but in other cases simple sample size formulas can be obtained similar to the ones we derived in Chapter 8 for fixed-width confidence in-tervals.

TABLE 9.3. nQuery Advisor 4.0 Table for 3:1 and 1:1 Sample Size Ratios for Tendril DX Trial Design