Missing Data and Imputation

MISSING DATA AND IMPUTATION

In the real world of clinical trials, protocols sometimes are not completed, or patients may drop out of the trial for reasons of safety or for obvious lack of efficacy. Loss of subjects from follow-up studies sometimes is called censoring. The missing data are referred to as censored observations. Dropout creates problems for statistical inference, hypothesis testing, or other modeling techniques (including analysis of variance and regression, which are covered later in this text). One approach, which ignores the missing data and does the analysis on just the patients with com-plete data, is not a good solution when there is a significant amount of missing data.

One problem with ignoring the missing data is that the subset of patients consid-ered (called completers) may not represent a random sample from the population. In order to have a representative random sample, we would like to know about all of the patients who have been sampled. Selection bias occurs when patients are not missing at random. Typically, when patients drop out, it is because the treatment is not effective or there are safety issues for them.

Many statistical analysis tools and packages require complete data. The com-plete data are obtained by statistical methods that use information from the avail-able data to fill in or “impute” values to the missing observations. Techniques for doing this include: (1) last observation carried forward (LOCF), (2) multiple impu-tation, and (3) techniques that model the mechanism for the missing data.

After imputation, standard analyses are applied as if the imputed data represent-ed real observations. Most techniques attempt to adjust for bias, and some deal with the artificial reduction in variance of the estimates. The usefulness of the methods depends greatly on the reasonableness of the modeling assumptions about how the data are missing. Little and Rubin (1987) provide an authoritative treatment of the imputation approaches and the statistical issues involved.

A second problem arises when we ignore cases with partially censored data: a significant proportion of the incomplete records may have informative data even though they are incomplete. Working only with completers throws out a lot of po-tentially useful data.

In a phase II clinical study, a pharmaceutical company found that patient dropout was a problem particularly at the very high and very low doses. At the high doses, safety issues relating to weight gain and lowering of white blood cell counts caused patients to drop out. At the low doses, patients dropped out because the treatment was ineffective.

In this case, the reason for missing data was related to the treatment. Therefore, some imputation techniques that assume data are missing in a random manner are not appropriate. LOCF is popular at pharmaceutical companies but is reasonable only if there is a slow trend or no trend in repeated observations over time. If there is a sharp downward trend, the last observation carried forward would tend to over-estimate the missing value. Similarly, a large upward trend would lead to a large underestimate of the missing value. Note that LOCF repeats the observation from the previous time point and thus implicitly assumes no trend.

Even when there is no trend over time, LOCF can grossly underestimate the variability in the data. Underestimation of the variability is a common problem for many techniques that apply a single value for a missing observation. Multiple impu-tation is a procedure that avoids the problem with the variance but not the problem of correlation between the measurement and the reason for dropout.

As an example of the use of a sophisticated imputation technique, we consider data from a phase II study of patients who were given an investigational drug. The study examined patients’ responses to different doses, including any general health effects. One adverse event was measured in terms of a laboratory measurement and low values led to high dropouts for patients. Most of these dropouts occurred at the higher doses of the drug.

To present the information on the change in the median of this laboratory mea-surement over time, the statisticians used an imputation technique called the incre-mental means method. This method was not very reliable at the high doses; there were so few patients in the highest dose group remaining in the study at 12 weeks that any estimate of missing data was unreliable. All patients showed an apparent sharp drop that might not have been real. Other methods exaggerated the drop even more than the incremental means method. The results are shown in Figure 9.3. The groups are labeled placebo and from A to E in order of increasing dose. 

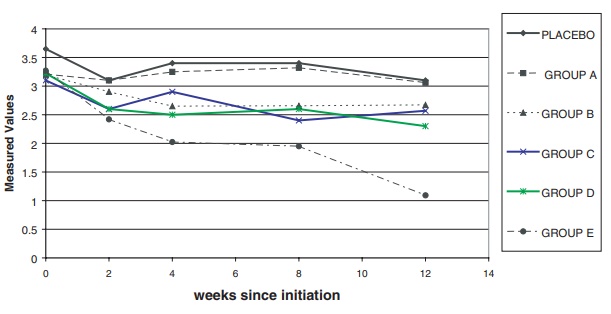
Figure 9.3. Laboratory measurements (median over time) imputed.

The figure shows that laboratory measurements apparently remained stable over time in four of the treatment groups in comparison to the placebo group, with the exception of the highest dose group (Group E), which showed an apparent decline. However, the decline is questionable because of the small number of patients in that group who were observed at 12 weeks.