Testing the Difference between Two Proportions
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Inferences Regarding Proportions
In testing the difference between two proportions, we have at our disposal exact binomial methods.
TESTING THE DIFFERENCE BETWEEN TWO PROPORTIONS
In testing the difference between two proportions,
we have at our disposal exact binomial methods. The software companies listed
in the previous section also provide solutions to this problem. In addition, we
can use Fisher’s exact test (described in Chapter 14). Now, as another
solution, we will provide the normal approximations for testing the difference
between two proportions and give an example.
Let W1
= X1/n1 and W2
= X2/n2, where X1
is binomial with parameters p1
and n1 and where X2 is binomial with
parameters p2 and n2. Note that p1 and p2 refer to popula-tion proportions. We are interested
in the difference between these two proportions p1 – p2. This difference can be
estimated by W1 –
W2. Now, the standard deviation for W1 – W2 is √[p1(1 – p1)/n1 + p2(1 – p2)/n2]
because the variance of W1 –
W2 is the sum of the individual variances. Each of
the variance terms under the radical is simply an analog of the variance for a
single proportion, as shown previously in Equation 10.4.
So a choice for Z would be Z = {W1 – W2 – (p1 –p2)}/
√[p1(1 – p1)/n1 + p2(1
– p2)/n2].
However, this equation is impractical because p1 and p2 are unknown. One way to obtain an approximation that
will yield a Z that has approximately
a standard nor-mal distribution would be to use the unbiased and consistent
estimates W1 and W2 in place of p1 and p2, respectively, everywhere in the denominator. Z is then a piv-otal quantity that can
be used for hypothesis testing or for confidence intervals.
The usual null hypothesis is that p1 = p2 or p1
– p2 = 0. So under H0: Z = (W1 – W2)/ √[W1(1 – W1)/n1 + W2(1 – W2)/n2]
is the test statistic with an approximately
standard normal distribution.
Now, W1
= X1/n1 and W2
= X2/n2. Under the null hypothesis, p1 = p2
= p; consequently, W1 and W2 have the same binomial parameter p. In this case, it makes sense to combine the data and Xc = X1 + X2
is binomial with parameters n1 + n2 and p. Then Wc = Xc/(n1 +
n2) is a natural estimate for
p and has greater pre-cision than either W1 or W2.
This estimate Wc is reasonable
only under the null hypothesis, however. Using this argument, we can make a
case that Z’ = (W1
– W2)/ √[Wc(1 – Wc)/n1 + Wc(1 – Wc)/n2]
is better to use, since the denominator gives a better estimate of the standard error of W1 – W2
when the null hypothesis is true. It simplifies to Z’ = (W1 – W2)/
√[Wc(1 – Wc)[(1/n1) + (1/√n2)]. This formula will not apply
when we are generating approximate confidence intervals.
The Z
test for the difference between two proportions p1 – p2
is
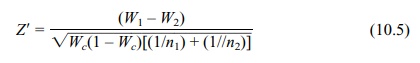
Z’ = (W1
– W2) / √{Wc(1 – Wc)[(1/n1) + (1//n2)]} (10.5)
where H0:
p1 = p2 = p, Xc = X1 + X2,
and Wc = Xc/(n1 + n2).
To illustrate, suppose n1 = 10, n2
= 9, X1 = 7, and X2 = 5. Then W1 = 7/10 = 0.700, W2 = 5/9 = 0.556, and Wc = 12/19 = 0.632. Then Z = (0.700 – 0.556)/ ( √{(0.632(0.368)[(1/10) + (1/9)]} = 0.134/ √{0.233[19/90]}
= 0.134/ √{0.233(0.211)} = 0.134/√0.049 = 0.134/0.222 = 0.604. This
difference is not statistically significant. Using the normal approximation we
see from the standard normal table that P[|Z| > 0.604] = 2P[Z > 0.604] = 2(0.5 –
P[0 < Z < 0.604]) ≈ 2(0.5 – P[0 < Z < 0.6]) = 1
– 2P[0 < Z < 0.6] = 1 – 2(0.2257) = 1 – 0.4514 = 0.5486. So the p-value is greater than 0.5.
Related Topics
