Procedures for Ranking Data
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Nonparametric Methods
Ranking data becomes useful when we are dealing with inferences about two or more populations and believe that parametric assumptions such as the normality of their distributions do not apply.
PROCEDURES FOR RANKING DATA
Ranking data becomes useful when we are dealing
with inferences about two or more populations and believe that parametric
assumptions such as the normality of their distributions do not apply. Suppose,
for example, that we have two samples from two distinct populations. Our null
hypothesis is that the two populations are identical. You may think of this as
stating that they have the same medians. We are not checking for differences in
means because the mean may not even exist for these populations. Table 14.1
shows how to rank data from two populations.
Let us denote the sample from the first population
with n1 observations x1, x2, x3,
. . . , xn1.
The second sample consists of n2
observations. For the purpose of the analysis, we will pool the data from the
two samples. We will label the observations from the second sample xn1+1, xn1+2, xn1+3, . . . , xn1+n2. Now, to rank the data, we or-der the observations from
smallest to largest and denote the ordered observations as y’s. If x5 is the smallest observation, x5 becomes y1,
and if x3 is the next smallest, x3 becomes y2,
and so forth. We continue in this way until all the x’s are assigned to all the y’s.
TABLE 14.1. Terminology for Ranking Data from Two Independent Samples

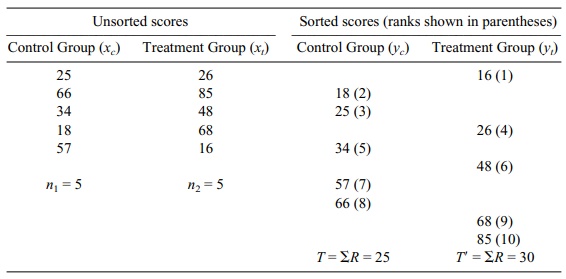
In Table 14.2, we present hypothetical data to
illustrate ranking. The y’s refer to
the ranked observations from the first and second samples. We have two groups,
control and treatment, xc
and xt, respectively.
To illustrate the procedures described in the
previous paragraph, suppose a re-searcher conducted a study to determine
whether physical therapy increased the weight lifting ability of elderly male
patients. As the researcher believed that the data were not normally
distributed, a nonparametric test was applied. The data un-der the unsorted
scores column represent the values as they were collected directly from the
subjects. Then the two data sets were combined and sorted in ascending order.
Each score was then assigned a rank, which is shown in parentheses. (Refer to
the columns labeled “sorted scores.”) The term ΣR means
that we should sum the ranks in a particular column; the symbols T and T’ refer to the sum of the ranks in
the control and treatment groups, respectively. In this example, T = 25 and T’ = 30. We do not need to keep
track of both of these statistics because the sum of all the ranks is T + T
’ and is known to be n(n
+ 1)/2, where n is the sum of the
sample sizes in the two groups, in this case n = 2(5) = 10, and so the sum of the ranks is 10(11)/2 = 55. In
summing all the ranks we are just adding up the integers from 1 to 10 in our
example.
A possible ambiguity can occur when some data
points share the same value. In that case, the ordering among the tied values
can be done by any system (e.g., choose the lowest indexed x first). Rather than assigning them separate ranks in ar-bitrary
order, sometimes we prefer to give all the tied observations the same rank.
That rank would be the average rank among the tied observations. If, for
example, the 3rd, 4th, 5th, and 6th smallest values were all tied, they would
all get the rank of 4.5 [i.e., (3 + 4 + 5 + 6)/4].
TABLE 14.2. Left Leg Lifting Test Data among Elderly Male Patients Who
Are Receiving Physical Therapy; Maximum Weight (Unsorted, Sorted, and Ranked)
For Treatment and Control Groups
Now that the x’s have been rearranged from the smallest to the largest values (the arrangement is sometimes called the rank order), the rank transformation is made by replacing the value of
the observation with its y
sub-script. This subscript is called the rank of the observation. Refer to
Table 14.1 for an example. You can see that the lowest rank is y1. If x5 is the smallest observation, its rank would be 1. If x3 and x9 are tied, they both would be assigned to y2 and y3 and have a rank of 2.5.
If the two distributions of the parent populations
are the same, then the ranks will be well mixed among the populations (i.e.,
both groups should have a similar num-ber of high and low ranks in their
respective samples). However, if the alternative is true (that the population
distributions are different) and the median or center of one distribution is
very different from the other, the group with the smaller median should tend to
have more lower ranks than the group with the higher median. A test statistic
based on the ranks of one group should be able to detect this difference. In
Section 14.3, we will consider an example: the Wilcoxon rank-sum test.
Related Topics
