Conjugated Π Systems

CONJUGATED π SYSTEMS

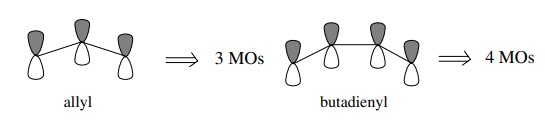
Another way to describe delocalized bonding uses the MO approach. The same principles of overlap of AOs can be applied to systems where more than two p AOs overlap to form π systems. First, the number of MOs produced by the overlap will be the same as the number of atomic p orbitals which interact. Thus for the allyl system where three contiguous p orbitals interact, there will be three MOs produced from the interaction of three 2p AOs. For the butadienyl system where there are four contiguous p orbitals interacting, four MOs will result, and so on.

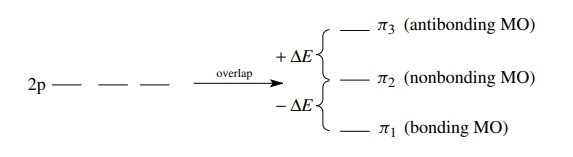
Second, the energy distribution of the MOs will be disposed symmetrically about the energy of the AOs before they interact (nonbonded energy level). This means that the total energy of the bonding MOs is offset by the total energy of the antibonding MOs. For example, if one MO is of lower energy by –ΔE due to overlap, then there must be an antibonding MO raised to higher energy (+ΔE). Molecular orbitals which are lower in energy than the nonbonding energy are bonding MOs, (−ΔE ), those which are higher in energy than the nonbonding energy are antibonding MOs (+ΔE), and those at the same energy as the nonbonding energy are nonbonding MOs (ΔE = 0).

For the allyl system which has 3 MOs from the overlap of three 2p AOs, one MO will be lowered in energy (−ΔE ) and so one MO will be raised by the same amount. The remaining MO must stay at the nonbonding level (ΔE = 0) to maintain energy symmetry around the nonbonding level.

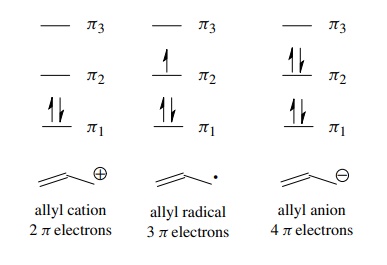
What is interesting is that this overlap model allows the orbital diagram to be constructed without concerning itself with electrons. The MOs produced by the interaction of AOs can each hold two paired electrons, and these can be filled in depending on the number of electrons present in the π system. Thus the bonding diagrams for the allyl cation, allyl radical, and allyl anion can be constructed by merely filling the orbitals with the number of π electrons present in these species (two, three, and four π electrons, respectively). This orbital picture also demonstrates that all three intermediates in the allyl system are stabilized because each contains two electrons in the π₁-bonding MO and any remaining electrons are in the nonbonding orbital.

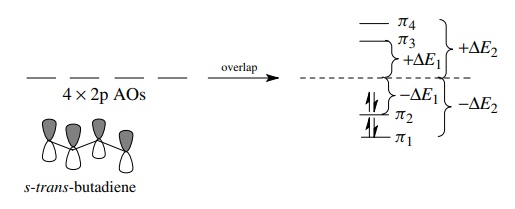
Two of the four MOs of the butadienyl system are at lower energy than the nonbonded energy level (−ΔE₁, − ΔE₂), and two are at higher energy than the nonbonded energy level (+ΔE₁, + ΔE₂). The four π electrons of butadiene fill the two bonding MOs and give a stable molecule. It should also be obvious that butadienyl species with less than or more than four π electrons should be significantly less stable than butadiene itself. Removal of an electron requires energy because the electron would have to come from a relatively stable bonding MO. Addition of an electron to the butadienyl π system requires that it be put into an antibonding MO which is also energetically unfavorable.

A great many π systems have been examined by this approach and the orbital diagrams understood. As seen before, the antibonding orbitals are often unfilled in the ground state but play an important part in the excited states and reactions of these compounds.