Confidence Intervals for the Difference between Means from Two Independent Samples (Variance Known)

CONFIDENCE INTERVALS FOR THE DIFFERENCE BETWEEN MEANS FROM TWO INDEPENDENT SAMPLES (VARIANCES KNOWN)

When the population variances are known, we use the Z statistic defined in the previous section, namely

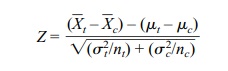
Z has exactly a standard normal distribution when the observations in both samples are normally distributed. Also, based on the central limit theorem, Z is approximately normal if conditions for the central limit theorem are satisfied for each population being sampled. For a 95% confidence interval we know that P(–C ≤ Z ≤ C) = 0.95 if C = 1.96. 

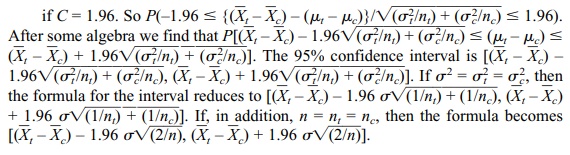
For other confidence levels, we just change the constant C to 1.645 for 90% or 2.575 for 99%. Display 8.4 pro-vides the formula for the 95% confidence interval for the difference between two population means, assuming common known population variance.