Point Estimates
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Estimating Population Means
Often the estimates are obvious, such as with the use of the sample mean to estimate the population mean.
POINT ESTIMATES
In Chapter 4, you learned about summary statistics.
We discussed population para-meters for central tendency (e.g., the mean,
median and the mode) and for disper-sion (e.g., the range, variance, mean
absolute deviation, and standard deviation). We also presented formulas for
sample analogs based on data from random samples taken from the population.
These sample analogs are often also used as point esti-mates of the population
parameters. A point estimate is a single value that is chosen as an estimate
for a population parameter.
Often the estimates are obvious, such as with the
use of the sample mean to estimate the population mean. However, sometimes we
can select from two or more possible estimates. Then the question becomes which
point estimate should you use?
Statistical theory offers us properties to compare
point estimates. One important property is consistency. The property of
consistency requires that as the sample size becomes large, the estimate will
tend to approximate more closely the population parameter.
For example, we saw that the sampling distribution
of the sample mean was cen-tered at the true population mean; its distribution
approached the normal distribu-tion as the sample size grew large. Also, its
variance tended to decrease by a factor of 1/ √n as the
sample size n increased. The sampling
distribution was concentrated closer and closer to the population mean as n increased.
The facts stated in the foregoing paragraph are
sufficient to demonstrate consis-tency of the sample mean. Other point estimates,
such as the sample standard devi-ation, the sample variance, and the sample
median, are also consistent estimates of their respective population
parameters.
In addition to consistency, another property of
point estimates is unbiasedness. This property requires the sample estimate to
have a sampling distribution whose mean is equal to the population parameter
(regardless of the sample size n).
The sample mean has this property and, therefore, is unbiased. The sample
variance (the estimate obtained by dividing by n – 1) is also unbiased, but the sample standard de-viation is not.
To review:
E![]() = μ (The sample mean is an unbiased estimate of the population
mean.)
= μ (The sample mean is an unbiased estimate of the population
mean.)
E(S2)
= σ 2 where S2 =
Σ n i=1 (Xi – ![]() )2/(n – 1) (The sample variance is an
unbiased estimate of the population
variance.)
)2/(n – 1) (The sample variance is an
unbiased estimate of the population
variance.)
E(S) ≠ σ (The
sample standard deviation is a biased estimate of the population standard deviation.)
Similarly S/√n is the usual estimate of the standard error of the mean, namely, σ/√n. However, since E(S) ≠ σ it also follows that E(S/√n) ≠ σ/√n. So our estimate of the standard error of the mean is also biased.
These results are summarized in Display 8.1.
If we have several estimates that are unbiased,
then the best estimate to choose is the one with the smallest variance for its
sampling distribution. That estimate would be the most accurate. Biased
estimates are not necessarily bad in all circumstances. Sometimes, the bias is
small and decreases as the sample size increases. This situa-tion is the case
for the sample standard deviation.
An estimate with a small bias and a small variance can be better than an estimate with no bias (i.e., an unbiased estimate) that has a large variance. When comparing a biased estimator to an unbiased estimator, we should consider the accuracy that can be measured by the mean-square error.
Display 8.1. Bias Properties of Some Common
Estimates
E(X) =
μ : The sample mean is an unbiased estimator of the
population mean.
E(S2) = σ2 : The sample
variance is an unbiased estimator of the population variance.
E(S) ≠ σ : The sample standard deviation is a biased estimator of the popula-tion standard deviation.
The mean-square error is defined as MSE = β2 + σ2, where β is the bias of the estimator and σ 2 is the variance of the estimator. An unbiased
estimator has MSE = σ 2.
Here we will show an example in which a biased
estimator is better than an unbi-ased estimator because the former has a
smaller mean square error than the latter. Suppose that A and B are two estimates
of a population parameter. A is
unbiased and has MSE = σA2. We use the
subscript A to denote that σA2 is the variance
for estimator A. B is a biased estimate and has MSE
= βB2 + σB2 .
Here we use B as the sub-script for
the bias and βB2 to denote the variance for estimator B. Now if βB2 + σB2
< σA2, then B is a better estimate of the population
parameter than A. This situation
happens if σB2
< σ2A – βB2 . To illustrate this numerically, suppose A is an unbiased estimator for a parameter θ and A has a variance of 50. Now B
is a biased estimate of θ with a bias of 4 and a variance of 25. Then A has a mean square error of 50 but B has a mean square error of 16 + 25 = 41. (B’s variance is 25 and the square of the bias is 16.) Because 41 is less than 50, B is a better estimate of θ (i.e., it has a lower mean square error).
As another example, suppose A is an unbiased estimate for θ with variance 36 and B is a
biased estimate with variance 30 but bias 4. Which is the better estimate?
Surprisingly, it is A. Even though B has a smaller variance than A, B
tends to be far-ther away from θ than A. In this case, B is more precise but misses the target,
where-as A is a little less precise
but is centered at the target. Numerically, the mean square error for A is 36 and for B it is 30 + (4)2 = 30 + 16 = 46. Here, a biased
estimate with a lower variance than an unbiased estimate was less accurate than
the unbiased esti-mator because it had a higher mean square error. So we need
the mean square error and not just the variance to determine the better
estimate when comparing unbiased and biased estimates. (See Figure 8.1.)
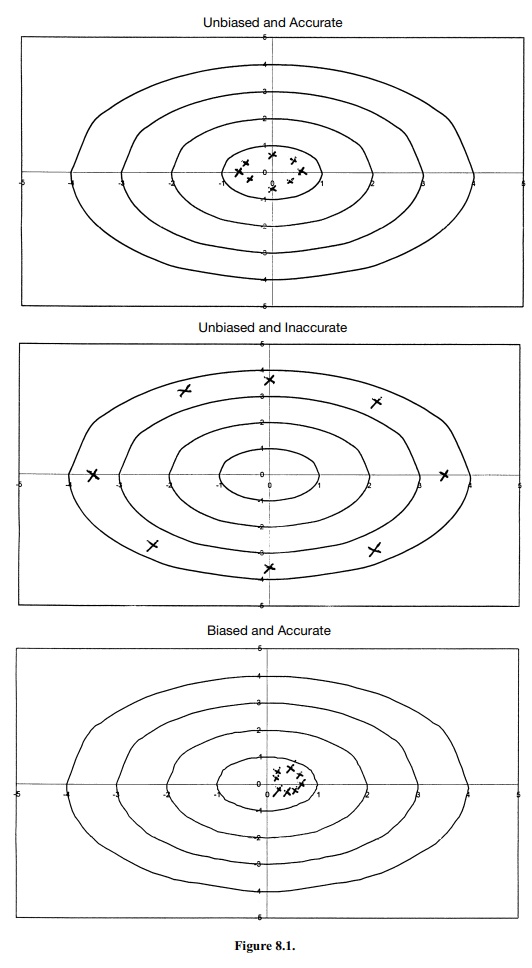
In conclusion, precise estimates with large bias
are never desirable, but precise estimates with small bias can be good.
Unbiased estimates that are precise are good, but imprecise unbiased estimates
are bad. The trade-off between accuracy and pre-cision is well expressed in one
quantity: the mean square error.
Related Topics
