Z Distribution Obtained When Standard Deviation Is Known

Z DISTRIBUTION OBTAINED WHEN STANDARD DEVIATION IS KNOWN

Recall that if X has a normal distribution with mean m and standard deviation σ, then the transformation Z = (X – μ)/σ leads to a random variable Z with a standard normal distribution. We can do the same for the sample mean X. Assume n is large so that the sample mean has an approximate normal distribution. Now, let us pretend for the mo-ment that the distribution of the sample mean is exactly normal. This is reasonable since it is approximately so. Then define the standard or normal Z score as follows:

Then Z would have a standard normal distribution because  has a normal distribution with mean μ = μ and standard deviation σ/√n.

Because in practice we rarely know σ, we can approximate σ by the sample estimate,

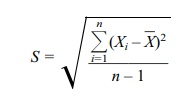
For large sample sizes, it is acceptable to use S in place of σ; under these conditions, the standard normal approximation still works. So we use the following formula for the approximate Z score for large sample sizes:

However, in small samples such as n < 20, even if the observations are normally distributed, using Formula 7.2 does not give a good approximation to the normal distribution. In a famous paper under the pen name Student, William S. Gosset found the distribution for the statistic in Formula 7.2 and it is now called the Stu-dent’s t statistic; the distribution is called the Student’s t distribution with n – 1 de-grees of freedom. This is the subject of the next section.