Exercises questions answers

EXERCISES

5.1 By using a computer algorithm, an investigator can assign members of twin pairs at random to an intervention condition in a clinical trial. Assume that each twin pair consists of dizygotic twins (one male and one female). The probability of assigning one member of the pair to the intervention condition is 50%. Among the first four pairs, what is the probability of assigning to the intervention condition: 1) zero females, 2) one female, 3) two females, 4) three females, 4) four females?

5.2 In this exercise, we would like you to toss four coins at the same time into the air and record and observe the results obtained for various numbers of coin tosses. Count the frequencies of the following outcomes: 1) zero heads, 2) one head, 3) two heads, 4) three heads, 5) four heads.

a. Toss the coins one time (and compare to the results obtained in Exercise 5.1).

b. Toss the coins five times.

c. Toss the coins 15 times.

d. Toss the coins 30 times.

e. Toss the coins 60 times.

5.3 In the science exhibit of a museum of natural history, a coin-flipping machine tosses a silver dollar into the air and tallies the outcome on a counting device. What are all of the respective possible outcomes in any three consecutive coin tosses? In any three consecutive coin tosses, what is the probability of: a) at least one head, b) not more than one head, c) at least two heads, d) not more than two heads, e) exactly two heads, f) exactly three heads.

5.4 A certain laboratory animal used in preclinical evaluations of experimental catheters gives birth to only one offspring at a time. The probability of giving birth to a male or a female offspring is equally likely. In three consecutive pregnancies of a single animal, what is the probability of giving birth to: (a) two males and one female, (b) no females, (c) two males first and then a fe-male, and (d) at least one female. State how the four probabilities are different from one another. For the foregoing scenario, note all of the possible birth outcomes in addition to (a) through (d).

5.5 What is the expected distribution—numbers and proportions—of each of the six faces (i.e., 1 through 6) of a die when it is rolled 1000 times?

5.6 A pharmacist has filled a box with six different kinds of antibiotic capsules. There are a total of 300 capsules, which are distributed as follows: tetracy-cline (15), penicillin (30), minocycline (45), Bactrim (60), streptomycin (70), and Zithromax (80). She asks her assistant to mix the pills thoroughly and to withdraw a single capsule from the box. What is the probability that the cap-sule selected is: a) either penicillin or streptomycin, b) neither Zithromax nor tetracycline, c) Bactrim, d) not penicillin, e) either minocycline, Bactrim, or tetracycline?

5.7 In an ablation procedure, the probability of acute success (determined at com-pletion of the procedure) is 0.95 when an image mapping system is used. Without the image mapping system, the probably of acute success is only 0.80. Suppose that Patient A is given the treatment with the mapping system and Patient B is given the treatment without the mapping system. Determine the following probabilities:

a.     Both patients A and B had acute successes.

b.      A had an acute success but B had an acute failure.

c.      B had an acute success but A had an acute failure.

d.     Both A and B had acute failures.

e.      At least one of the patients had an acute success.

f.       Describe two ways that the result in (e) can be calculated based on the re-sults from (a), (b), (c), and (d).

5.8 Repeat Exercise 5.4 but this time assume that the probability of having a male offspring is 0.514 and the probability of having a female offspring is 0.486. In this case, the elementary outcomes are not equally likely. However, the trials are Bernoulli and the binomial distribution applies. Use your knowledge of the binomial distribution to compute the probabilities [(a) through (e) from Exercise 5.5].

5.9 Refer to Formula 5.7, permutations of r objects taken from n objects. Compute the following permutations:

a.     P(8, 3)

b.     P(7, 5)

c.      P(4, 2)

d.     P(6, 4)

e.      P(5, 2)

5.10 Nine volunteers wish to participate in a clinical trial to test a new medication for depression. In how many ways can we select five of these individuals for assignment to the intervention trial?

5.11 Use Formula 5.8, combinations of r objects taken out of n, to determine the following combinations:

a.     C(7, 4)

b.     C(6, 4)

c.      C(6, 2)

d.     C(5, 2)

e.      What is the relationship between 5.11 (d) and 5.9 (e)?

f.       What is the relationship between 5.11 (b) and 5.9 (d)?

5.12 In how many ways can four different colored marbles be arranged in a row?

5.13 Provide definitions for each of these terms:

a.     Elementary events

b.     Mutually exclusive events

c.      Equally likely events

d.     Independent events

e.      Random variable

5.14 Give a definition or description of the following:

a.     C(4, 2)

b.     P(5, 3)

c.The addition rule for mutually exclusive events

d.     The multiplication rule for independent events

5.15 Based on the following table of hemoglobin levels for miners, compute the probabilities described below. Assume that the proportion in each category for this set of 90 miners is the true proportion for the population of miners.

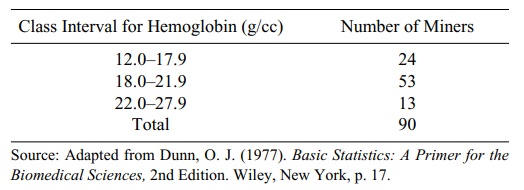
a.     Compute the probability that a miner selected at random from the population has a hemoglobin level in the 12.0–17.9 range.

b.     Compute the probability that a miner selected at random from the population has a hemoglobin level in the 18.0–21.9 range.

c.      Compute the probability that a miner selected at random from the population has a hemoglobin level in the 22.0–27.9 range.

d.     What is the probability that a miner selected at random will have a hemoglobin count at or above 18.0?

e.      What is the probability that a miner selected at random will have a hemoglobin count at or below 21.9?

f. If two miners are selected at random from the “infinite population” of min-ers with the distribution for the miners in the table, what is the probability that one miner will fall in the lowest class and the other in the highest (i.e., one has a hemoglobin count in the 12.0 to 17.9 range and the other has a hemoglobin count in the 22.0 to 27.9 range)?

5.16 Consider the following 2 × 2 table that shows incidence of myocardial infarc-tion (denoted MI) for women who had used oral contraceptives and women who had never used oral contraceptives. The data in the table are fictitious and are used just for illustrative purposes.

Assume that the proportions in the table represent the “infinite population” of adult women. Let A = {woman used oral contraceptives} and let B = {woman had an MI episode}

a.     Find P(A), P(B), P(A^c), and P(B^c).

b.     What is P(A ∩ B)?

c.      What is P(A U B)?

d.     Are A and B mutually exclusive?

e.      What are P(A|B) and P(B|A)?

f. Are A and B independent?

5.17 For the binomial distribution, do the following:

a.     Give the conditions necessary for the binomial distribution to apply to a random variable.

b.     Give the general formula for the probability of r successes in n trials.

c.      Give the probability mass function for Bi(10, 0.40).

d.     For the distribution in c, determine the probability of no more than four successes.

5.18 Sickle cell anemia is a genetic disease that occurs only if a child inherits two recessive genes. Each child receives one gene from the father and one from the mother. A person can be characterized as follows: The person can have: (a) two dominant genes (cannot transmit the disease to a child), (b) one domi-nant and one recessive gene (has the trait and is therefore a carrier who can pass on the disease to a child, but does not have the disease), or (c) has both recessive genes (in which case the person has the disease and is a carrier of the disease). For each parent there is a 50–50 chance that the child will inher-it either the dominant or the recessive gene. Calculate the probability of the child having the disease if:

a.     Both parents are carriers

b.     One parent is a carrier and the other has two dominant genes

c.      One parent is a carrier and the other has the disease

Calculate the probability that the child will be a carrier if:

d.     Both parents are carriers

e.      One parent is a carrier and the other has the disease

f.       One parent is a carrier and the other has two dominant genes

5.19 Under the conditions given for Exercise 5.18, calculate the probability that the child will have two dominant genes if:

a.     One of the parents is a carrier and the other parent has two dominant genes

b.     Both of the parents are carriers

5.20 Compute the mean and variance of the binomial distribution Bi(n, p). Find the arithmetic values for the special case in which both n = 10 and p = 1/2.

5.21 a. Define the probability density and cumulative probability function for an absolutely continuous random variable.

b. Which of these functions is analogous to the probability mass function of a discrete random variable?

c. Determine the probability density function and the cumulative distribution function for a uniform random variable on the interval [0, 1].

5.22 In the example in Section 5.9, consider the probability that three items have mismatched labels and one of these items is found.

a.     Calculate the probability that all three items would pass inspection and, therefore, there would be two additional ones out of the 84 remaining in the field.

b.     Calculate the probability that exactly one of the two remaining items with mismatched labels is among the 84 items still in the field. (Hint: Add to-gether two probabilities, namely the probability that exactly one item is re-moved at the second stage but none at the third, added to the probability that exactly one item is removed at the third stage but none at the second).

c.      Use the results from (a) and (b) above to calculate the probability that at least one of the two additional items with mismatched labels is among the 84 remaining in the field.

d.     Based on the result in (c), do you think the probability is small enough not to recall the 84 items for inspection?

Answers:

5.1 The probability of no females and 4 males is the same as getting 4 heads in a row tossing a fair coin or (1/2)⁴ = 1/16 = 0.0625. To get one female we could have the sequence FMMM, which has probability 1/16 also, but there are C ⁴₁ = 4!/(1! 3!) = 4 ways of arranging 1 female and 3 males. These 4 mutually exclusive cases each have probability 1/16. taking the sum the probability is 4/16 = 1/4 = 0.250 for 1 fe-male. For 2 females and 2 males there are C⁴₂ = 4!/(2! 2!) = 6 ways of getting 2 males and 2 females. So the probability is 6/16 = 3/8 = 0.375. For 3 females, we again have 4 ways of getting 3 females and 1 male, so the probability is 0.250 for 3 females. Finally, the probability of getting all 4 females is the same as the probabil-ity of 0 heads when tossing a fair coin, or 1/16 = 0.0625.

5.5 Each of the six faces of a balanced die has the same chance as any other. So the probability is 1/6 for a single dot, 1/6 for two dots, 1/6 for three dots, 1/6 for four dots, 1/6 for five dots and 1/6 for the face with six dots. These probabilities also represent the expected proportion of occurrences for each of these respective faces in 1000 rolls. The expected number of occurrence is simply np, where n is the number of rolls and p is the probability of occurrence on an individual roll. Since in this example n = 1000 and p = 1/6, the expected numberis 166.67 for each of the six faces.

5.11 a. This is the number of combinations of seven objects chosen four at a time: C(7, 4) = 7!/(4!3!) = 7 × 6 × 5/(3 × 2) = 35.

b. This is the number of combinations of six objects chosen four at a time: C(6, 4) = 6!/(4!2!) = 6 × 5/2 = 15.

c. This is the number of combinations of six objects chosen two at a time: C(6,2) = 6!/(2!4!) = 6 × 5/2 = 15. This gives the same result as b.

d. This is the number of combinations of five objects chosen two at a time: C(5, 2)  = 5!/(2!3!) = 5 × 4/2 = 10.

e. 5.11 d is C(5, 2), the number of combinations of five objects chosen two at a time, whereas 5.9 e is P(5, 2), the number of permutations of five objects chosen two at a time. The difference between permutations and combinations is that in per-mutations the order matters, whereas in combinations it does not. So if the five ob-jects are labeled a, b, c, d, and e. There is only one combination for the choice of a and b but there are two permutations, namely, ab, and ba. This is true for each dis-tinct pair. So P(5, 2) is 2C(5, 2). In general, C(n, r) = P(n, r)/P(r, r) = P(n, r)/r! Or P(n, r) = r! C(n, r). In this case, r = 2 and n = 5.

f. 5.11 b is C(6, 4), the number of combinations of six objects chosen four at a time, whereas 5.9 d is P(6, 4), the number of permutations of six objects chosen four at a time. From e, we saw that the difference here is the difference between permutations and combinations. From the general result given in e, we see that C(n, r) = P(n, r)/P(r, r) = P(n, r)/r! Or P(n, r) = r! C(n, r). In this case, r = 4 and n = 6. So P(6, 4) = 4! C(6, 4) = 24 C(6, 4).

5.12 Say that the colors are red, blue, green, and yellow, denoted R, B, G, and Y, respectively. The possible arrangements are the number of permutations 4! = 4 × 3 × 2 = 24. They are RBGY, RBYG, RGYB, RGBY, RYGB, RYBG, BRGY, BRYG, BGRY, BGYR, BYRG, BYGR, GRBY, GRYB, GBYR, GBRY, GYRB, GYBR, YRBG, YRGB, YGRB, YGBR, YBGR, YBRG.

5.14 a. C(4, 2) = 4!/(2!2!) = 4 × 3/2 = 6. This is the number of combinations of 4 objects taken 2 at a time.

b. P(5, 3) = 5!/2! = 5 × 4 × 3 = 60. This is the number of permutations of 5 ob-jects taken 3 at a time.

c. 4!=4×3×2=24.

d. P(A U B) = P(A) + P(B).

e. P(A ∩ B) = P(A) P(B).

5.20 If X is binomial with parameters n and p, then the expected value is the sum of the expected value on each Bernoulli trial, but if Y = 0 with probability 1 – p and Y = 1 with probability p, then E(Y) = (1 – p)0 + p(1) = p. Now E(X) = np since p is summed n times (n Ys are added together) the

Var(X) = E(X – np)² = Σ(k – np)²C(n, k)p^k(1 – p)^n–k = Σk²C(n, k)p^k(1 – p)^n-k – Σ2knpC(n, k)p^k(1 – p)^n–k + Σn²p²C(n, k)p^k(1 – p)^n–k

We now use a few simple tricks. First recall for any integer m > 0

ΣC(m, k)p^k(1 – p)^m–k = 1                   (1)

when the sum is taken from k = 0 to k = m. This is because it is the sum of probabil-ities for all possible outcomes of a binomial random variable with parameters m and p. We will repeatedly use equation (1). Next, for a binomial random variable X, we have seen

E(X) = np = ΣkC(n, k)p^k(1 – p)^n–k              (2)

We will also exploit equation (2).

Let us consider the third term in the variance formula first:

Σn²p²C(n, k)p^k(1 – p)^n–k = n²p²ΣC(n, k)p^k(1 – p)^n–k = n²p²

using equation (1).

Now consider the second term in the variance formula:

–Σ2knpC(n, k)p^k(1 – p)^n–k = –2npΣkC(n, k)p^k(1 – p)^n–k = –2n²p²

using equation (2).

So the variance equation reduces to

Var(X) = Σk²C(n, k)p^k(1 – p)^n–k – 2n²p² + n²p² = Σk²C(n, k)p^k(1 – p)^n–k – n²p²

Now we consider the first term. We use an algebraic trick:

Σk²C(n, k)p^k(1 – p)^n–k = ΣkC(n, k)p^k(1 – p)^n–k + Σk(k – 1)C(n, k)p^k(1 – p)^n–k

Now by (2) the first term is np. Consider the second term:

Σk(k – 1)C(n, k)p^k(1 – p)^n–k = Σ [ k(k – 1)n! / k!(n – k)! ] p^k(1 – p)^n–k

Notice that in the sum the terms k = 0 and k = 1 are both 0, so we can take the sum from k = 2 to n. Let m = n – 2 and j = k – 2. Substituting j and m in the equation above we get

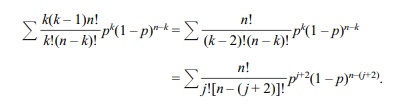
The sum on the right side of the above equation goes from j = 0 to j = m = n – 2. By factoring our n(n – 1)p² from the summation we get for the right side,

n(n – 1)p2  =  Σ [ (n – 2)!  / j!(n – 2 – j)! ] . p^j(1 – p)^n–2–j

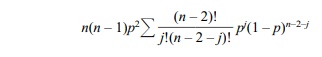
but this sum equals 1 by equation (1) applied with m = n – 2 > 0. Note equation (1) holds trivially for n – 2 = 0. So m = 0 is also acceptable. So for any n ≥ 2, Var(X) = np + n(n – 1)p² – n²p² = np + n²p² – np² – n²p² = np – np² = np(1 – p) For n = 10 and p = 1/2, the mean is 5 and the variance is 10(1/2)(1/2) = 5/2 = 2.5. Note that the proof does not include the case n = 1, a single Bernoulli trial. In that case, we com-pute the variance directly, namely, Var(X) = E[X – E(X)]² and E(X) = 0(1 – p) + 1(p) = p. So Var(X) = E(X – p)² = (1 – p)(0 – p)² + (p)(1 – p)² = (1 – p)p² + p(1 – p)² = p(1 – p)(p + 1 – p) = p(1 – p) = np(1 – p), since n = 1.