Exercises questions answers
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Analysis of Survival Times
Biostatistics for the Health Sciences: Analysis of Survival Times - Exercises questions answers
EXERCISES
15.1 Give definitions of the following terms in your
own words and indicate when it is appropriate to use each of them.
a. Life tables
b. The Kaplan–Meier curve
c. The negative exponential survival distribution
d. The Weibull distribution
e. Cure rate models
f. Log rank test
15.2 For a negative exponential survival function S(t),
recall that S(t) = exp(λt), where λ is the rate parameter or hazard rate function. Consider the conditional
probability that the survival time is T
> t2, given that we
know T > t1, where t1
< t2. Denote by S(t2|t1) the conditional
probability of survival be-yond t2,
given that the patient survives beyond t1,
i.e., P[T > t2|T > t1]. Show that S(t2|t1) = exp[λ(t2 – t1)]. The term exp[λ(t2 – t1)]
is called the lack of memory property of the negative exponential lifetime
model because the survival at time t1
has the same distribution as the survival at time 0; if τ = t2 - t1,
the probability of surviving τ units of time is the same at 0 as it is at t1, namely exp(λt). The probability of surviving depends only on τ and not on the time t1 that we are conditioning
on.
15.3 If the survival function S(t) = 1 – t/b for 0 ≤ t ≤ b for a fixed positive con-stant b, calculate the hazard function h(t) for 0 ≤ t ≤ b.
Recall that F(t) = 1 - S(t) and f (t) is the derivative
of F with respect to t. By definition, h(t) = f (t)/S(t).
What is the lowest value for the hazard rate? Is there a highest val-ue for the
hazard rate? (Hint: Choose M large.
If there exists a c < b such that h(c) is greater than M and M is arbitrary, then there is no highest value for the hazard function.)
15.4 If the survival times in months for one group are
{7.5, 12, 16, 33+, 55, 61} and {31, 60, 65, 76+, 80+,
92} for the second group, apply the chi-square test to see if the survival
curves are significantly different from one another. Re-call that the notation
of a plus as a superscript on the number indicates cen-soring at the denoted
time, namely at 33 months for the case in group 1 and at 76 and 80 months for
the cases in group 2. Test at the 0.01 significance level. Does the result seem
obvious just from looking at the data?
15.5 Suppose the survival times (in months since
transplant) for eight patients who received bone marrow transplants are 3.0,
4.5, 6.0, 11.0, 18.5, 20.0, 28.0, and 36.0. Assume no censoring.
a. What is the median survival time?
b. What is the mean survival time?
c. Using 5 months as the interval, construct a life table for these data.
15.6 Using the data in Exercise 15.5,
a. Calculate a Kaplan–Meier curve for the survival distribution.
b. Fit a negative exponential survival model to the data.
c. Compare the fitted exponential to the Kaplan–Meier curve at the eight
event times.
d. Based on the comparison in c, would you say the exponential is a good
fit?
15.7 Again, we use the data from Exercise 15.5, but we
assume that 6.0, 18.5, and 28 are censor times.
a. Estimate the median survival time.
b. Why would an estimate of the mean survival time based on averaging all
the times be inappropriate?
c. Using 5 months as an interval, construct a life table for the data.
15.8 Using the data in Exercise 15.7, construct a
Kaplan–Meier estimate of the survival distribution.
15.9 Again using the data in Exercise 15.7, fit a
negative exponential model. Compare it to the Kaplan–Meier curve at the event
times 3, 4.5, 11.0, 20.0, and 36.0 months, and decide whether or not the
negative exponential pro-vides a good fit.
15.10 Using a chi-square test, formally test the goodness
of fit of the negative ex-ponential distribution obtained in Exercise 15.9.
Test at the 0.05 level of sig-nificance.
15.11 Listed below in units of months are the survival
and censor times (censoring denoted
by a superscripted plus sign) for six males and six females.
Males: 1, 3, 4+, 9, 11, 17
Females: 1, 3+, 6, 9, 10, 11+
a. Calculate a Kaplan–Meier curve for the males.
b. Calculate a Kaplan–Meier curve for the females.
c. Apply a chi-square test to determine if the two survival curves differ
from one another.
15.12 For the data in Exercise 15.11:
a. Compute the mean survival time for males using all the observations
(in-cluding the censoring times).
b. Repeat part a for the females.
c. Compute the mean survival times for males and females, respectively,
using only the uncensored times.
d. Which estimate makes more sense if censoring can be considered to oc-cur
at random?
Answers:
15.2 S(t2|t1) = P{T > t2|T
> t1} = P{T > t2 ∩ T > t1}/P{T > t1}. Since t2 > t1, the event T > t2 is
contained in the event T > t1. Therefore P{T
> t2 ∩ T > t1} = P{T
> t2}. So S(t2|t1) = P{T > t2}/P{T > t1} = exp(λt2)/exp(λt1) = exp(λt2 – λt1) = exp[λ(t2 – t1)].
15.4 We get the expected and observed numbers for the
chi-square test from the following
table:
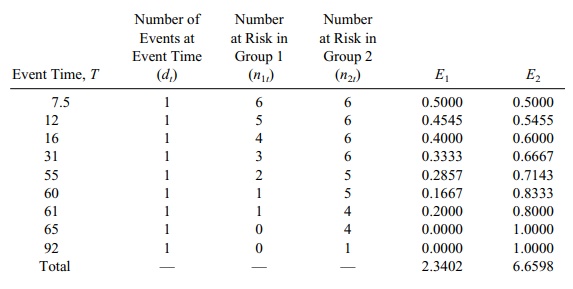
Now for the chi-square, we have the observed number
of 5 events for group 1 and 5 events for group 2. So χ2 = (5 – 2.3402)2/2.3402 + (5 – 6.6598)2/6.6598 =
3.437. This does not quite reach the 5% level of significance. The
distributions do appear to differ by inspection, but the sample size is small
(only 5 events in each group).
15.6 a. We generate the Kaplan–Meier curve using the
following table:
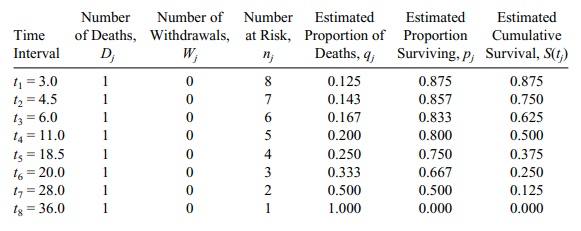
b and c. For the negative exponential, S(t)
= exp(–λt) and we
estimate time between failures 1/λ from the data as total time on test divided by the total number deaths
= (3.0 + 4.5 + 6.0 + 11.0 + 18.5 + 20.0 + 28.0 + 36.0)/8 = 127/8 = 15.875. So
the estimate for λ = 1/15.875 = 0.063.
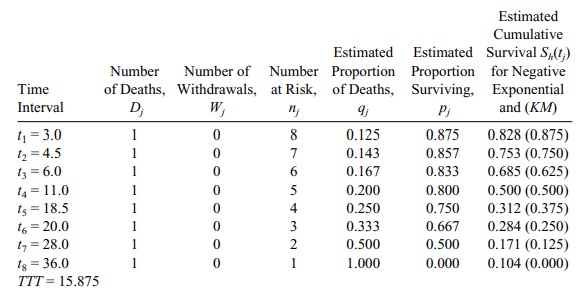
d. This exponential model seems to reasonably fit the
data.
15.8 Here we change the events at times 6.0, 18.5, and
28.0 to censored times rather than
event times. The corresponding Kaplan–Meier table looks as follows:
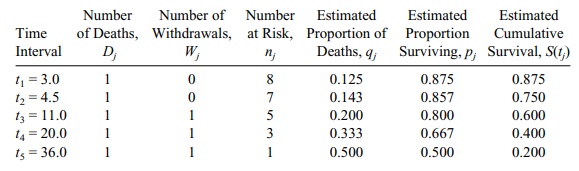
Related Topics
