Survival Probabilities: The Kaplan–Meier Curve
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Analysis of Survival Times
The Kaplan–Meier curve is a nonparametric estimate of the survival curve.
Survival Probabilities
The Kaplan–Meier Curve
The Kaplan–Meier curve is a nonparametric estimate
of the survival curve (see Ka-plan and Meier, 1958). It is computed by using
the same conditioning principle that we employed for the life table estimate in
Section 15.2.2. Because the Kaplan–Meier curve is an estimator based on the
products of conditional probabili-ties, it is also sometimes called the
product-limit estimator.
The Kaplan–Meier curve starts out with S(t)
= 1 for all t less than the first
event time (such as a death at t1).
Then S(t1) becomes S(0)
(n1 – d1)/n1,
where n1 is the number at
risk at time t1 and d1 is the number who die at
time t1. Referring to
Table 15.2 (column Sj,
first row), S(t1) = S(0) [(n1 – d1)/n1]
= 1[(10 – 1)/10] = 0.9. We sub-stitute Nj’ for n1
in the formula. At the next time of death t2,
S(t2)
= S(t1) (n2
– d2)/n2, where n2
and d2 are, respectively,
the corresponding number of patients at risk and deaths at time t2. In Table 15.2 (second
row), S(t2) = S(t1) [(n2 – d2)/n2] = (0.9)[(8.5 –2)/8.5] =
0.688. The estimate S(t) stays constant at all times between
events (i.e., deaths) but jumps down by the factor (nj – dj)/nj at the time tj of the jth deaths. You can verify this fact for
the Sj column in Table
15.2. We allow for the possibility of more than one death at the same instant
of time. The number at risk drops at with-drawal times as well as at the times
of death. Thus, we use Nj’ instead of Nj
to esti-mate nj in the
formula for S(t).
The Kaplan–Meier estimates can be portrayed in a
table similar to the life table (Table 15.2), except that the intervals will be
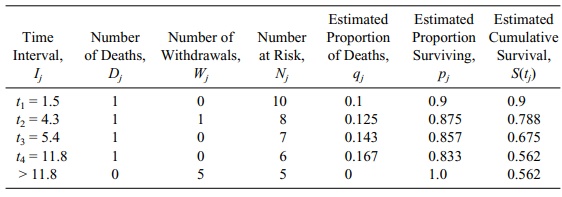
the times between events. Table 15.3 shows the Kaplan–Meier estimate for the
patient data used in the previous section to construct a life table. Note that
the column labels are essentially the same as those in Table 15.2, with the
following two exceptions: (1) the column labeled “Av-erage Number at Risk, Nj’,” has been eliminated; and (2) the “Estimated
Cumula-tive Survival” becomes S(tj), a term that we defined
in the foregoing paragraph.
In the row for t1
under the column “Estimated Cumulative Survival” we obtain 0.9 by multiplying S0 = 1 by p1 = 0.9, where p1 = 1 – q1 and q1
= D1/N1 = 1/10 = 0.1. In the row for t2, q2
= D2/N2 = 1/8 = 0.125. So p2
= 1 – q2 = 0.875 and,
finally, S2 =
TABLE 15.3. Kaplan–Meier Survival Estimates for Patients in Table 15.2
Approximate confidence intervals for the
Kaplan–Meier curve at specific time points can be obtained by using the
Greenwood formula for the standard error of the estimate and a normal
approximation for the distribution of the Kaplan–Meier esti-mate. A simpler
estimate is obtained based on the results in the paper by Peto et al. (1977).
In Greenwood’s formula, Var(Sj) is estimated as Vj
= S2j[Σij=1qi/(Nipi)].
Computationally, this is more easily calculated recursively as Vj = S2j[qj/(Nj pj)
+ Vj–1/S 2j–1], where we define S0 = 1 and V0
= 0.
Although the Greenwood formula is computationally
easy using the recursion equation, the Peto approximation is much simpler.
Peto’s estimate of variance is given by the formula Wj = S2j(1 – Sj)/Nj.
The simplicity of this formula is that it de-pends only on the survival
probability estimate at time j and
the number remaining at risk at time j,
whereas Greenwood’s formula depends on survival probability es-timates, number
at risk, and probability estimates of survival and death in preceding time
intervals.
Peto’s estimate has a heuristic interpretation. If
we ignore the censoring and think of failure by time j as a binomial outcome, to expect Nj patients to remain at time j we should have started with approximately Nj/Sj
patients. Think of this num-ber (Nj/Sj) as an integer
corresponding to the number of patients in a binomial ex-periment. Now the
variance of a binomial proportion is p(1
– p)/n, where n is the sample
size and p is the success probability.
In our heuristic argument, Sj
= p and Nj/Sj = n. So the variance is Sj(1 – Sj)/{Nj/Sj} = S2j(1
– Sj)/Nj. We see that this variance is just Peto’s formula.
The square root of these variance estimates
(Greenwood and Peto) is the corre-sponding estimate of the standard error of
the Kaplan–Meier estimate Sj
at time j. Approximate confidence
intervals then are obtained through a normal approxima-tion that uses the
normal distribution constants 1.96 for a two-sided 95% confidence interval or
1.645 for a two-sided 90% confidence interval. So the Greenwood 95% two-sided
confidence interval at time j would
be [Sj – 1.96 √Vj, Sj + 1.96 √Vj] and for Peto it would be [Sj
– 1.96 √Wj, Sj + 1.96 √Wj]. Greenwood’s and Peto’s meth
Display 15.1. Greenwood’s Method for 95% Confidence Interval of Kaplan–Meier Estimate
[Sj
– 1.96 √Vj, Sj +
1.96 √Vj]
where Sj = Kaplan–Meier survival probability estimate at the jth event time, and
Vj = S 2j [ Σj i=1 qi/(Ni pi)]
where qi is the probability of death in event interval i, pi
= 1 – qi is the probability
of surviving interval i, and Ni is the number of patients
remaining at risk at the ith event
time. Alternatively, Vj can
be calculated by the recursion:
Vj = S2j[qj/(Njpj)
+ Vj–1/S 2j–1]
ods are exhibited in Displays 15.1 and 15.2.
Because we have used several approxi-mations, these confidence intervals are
not exact, but only approximate.
Now we can construct 95% confidence intervals for
our Kaplan–Meier estimates in Table 15.3. Let us compute the Greenwood and Peto
intervals at time t3 =
5.4. For the Greenwood method, we must determine V3 first. We will do this using the recursive formula,
first finding V1, then V2 from V1, and finally V3
from V2. So V1 = S12[q1/(N1p1)] = (0.9)2 [0.1/(10(0.9)] = 0.9 (0.01) = 0.009. Then V2 = S22 [q2/(N2p2) + V1/S21] = (0.788)2 [0.125/(8 (0.875)) + 0.009/(0.9)2]
= 0.621 [0.125/7 + 0.009/0.81] 0.621(0.0179 + 0.0111) = 0.621(0.029) = 0.0180.
Finally, V3 = S23[q3/(N3 p3)
+ V2/S22] = (0.675)2 [0.143/{7(0.857)} + 0.018/(0.788)2]
= 0.4556 [0.143/6] = 0.0109. So the
95% confidence interval is [0.675 – 1.96 √0.0109,
0.675 + 1.96 √0.0109] = [0.675 –0.2046, 0.675 + 0.2046] = [0.4704, 0.8796].
For the Peto interval, W3 is simply S23(1
– S3)/N3 = (0.675)2(0.325/7) = 0.4556
Display 15.2. Peto’s Method for 95% Confidence Interval of
Kaplan–Meier Estimate
[Sj – 1.96 √Wj, Sj +
1.96 √Wj]
where Sj = Kaplan–Meier survival probability estimate at the jth event time, and
Wj = S2j(1 – Sj)/Nj
where Nj is the number of patients remaining at risk at the jth event time.
(0.0464) = So the Peto interval
is [0.675 – 1.96 √0.0212, 0.675 + 1.96 √0.0212] = [0.675 – 0.285, 0.675 + 0.285] = [0.390, 0.960]. Note that the
Peto interval is wider and thus somewhat more conservative for the lower
endpoint.
Some research [see Dorey and Korn (1987)] has shown
that Peto’s method can give better lower confidence bounds than Greenwood’s,
especially at long follow-up times in which the number of patients remaining at
risk is small. The Greenwood interval tends to be too narrow in these
situations; hence, the FDA sometimes rec-ommends using Peto’s method for the
lower bound. We have seen how the Peto in-terval is wider than the Greenwood
interval in the foregoing example. For more de-tails about the Kaplan–Meier
curve and life tables, see Altman (1991) and Lawless (1982).
As we can see from the example in Table 15.3, the
Kaplan–Meier curve gives re-sults similar to the life table method and is based
on the same computational princi-ple. However, the Kaplan–Meier curve takes
step decreases at the actual time of events (e.g., deaths), whereas the life
table method makes the jumps at the end of the group intervals.
The Kaplan–Meier curve is preferred to the life
table when all the event times are known precisely. For example, the Kaplan–Meier
method does a better job than the life table when dealing with withdrawals when
all withdrawals prior to an event (such as death) are removed in determining
the number of patients at risk. In con-trast, the life table groups the events
into time intervals; hence, it subtracts half the withdrawals in the interval
in order to estimate the interval survival (or failure) probability.
However, there are many practical situations in
which the event times are not known precisely but an interval for the event can
be defined. For example, recur-rence of some event may be detected at follow-up
visits, which could be scheduled every three months. All that is really known
is that the recurrence occurred between the last two follow-up visits. So a
life table with a three-month grouping may be more appropriate than a
Kaplan–Meier curve in such cases.
Although survival curves are very useful, some
difficulties occur when not all the events are reported. Lack of completeness
in reporting events is a common problem that medical device companies confront
when they report on the reliability of their products using Kaplan–Meier
estimates from passive databases (i.e., data-bases that depend on voluntary
reporting of problems). Such databases are notori-ous for underreporting events
and overestimating performance as estimated in the survival curve. Techniques
have been proposed to adjust these curves to account for biases. However, no
proposal is free from potential problems. See Chernick, Poulsen, and Wang
(2002) for a look at the problem of overadjustment with an al-gorithm that has
been suggested for pacemakers.
Related Topics
