Survival Probabilities: Cure Rate Models

Cure Rate Models

Cure rate models can be estimated by using the same survival data described in the previous section. However, in producing survival curves, we usually assume that the cumulative survival probability S(t) goes to zero as t approaches infinity. In cure rate models, we assume that some fraction of the patient population afflicted with a particular disease is actually cured, will not die, and will not experience a recur-rence. This proportion is called the cure fraction or cure rate. With a Kaplan–Meier curve, a cure rate would show up as a nonzero asymptote to the curve. By that we mean that the survival probability curve will flatten out at a value p equal to the cure rate.

Berkson and Gage (1952) first discussed a mixture model that is the most popular and easy to understand cure rate model. It assumes that a certain fraction p of the entire population will be cured by the treatment and the remaining 1 – p fraction of the population will not be cured. Equation 15.2 defines the mixture model for the population survivor function S(t) by using p and 1 – p:

S(t) = p + (1 – p)S*(t)                         (15.2)

Figure 15.1 shows a mixture survival curve with S*(t) representing an exponen-tial survival curve with rate 1 event per year and p, the cure proportion, equal to 0.2. for any t > 0, where p is the cure fraction and S*(t) is the survival function for the uncured subpopulation.

The survivor function S*(t) can be estimated by parametric or nonparametric methods. Maller and Zhou (1996) provide extensive treatment of cure models using the frequentist approach. Ibrahim, Chen, and Sinha (2001) cover cure models from the Bayesian perspective and provide many additional references. We will not pursue this topic further.

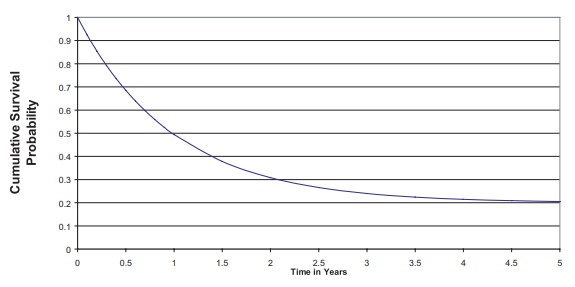
Figure 15.1. Exponential cure rate model with cure rate p = 0.2.

Although the concept of cure rates goes back to the 1950s, much of the research activity on this topic took place in the 1990s. Good algorithms for mixtures, such as the EM algorithm or a Markov chain Monte Carlo algorithm, became popular as re-cently as the 1980s and 1990s. Available at no charge, the software package Win-BUGS performs Gibbs sampling algorithms for Markov chain Monte Carlo appli-cations. (See Chapter 16.)