Exercises questions answers
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Nonparametric Methods
Biostatistics for the Health Sciences: Nonparametric Methods - Exercises questions answers
EXERCISES
14.1 Apply the Wilcoxon rank-sum test to the following
problem; we have modified the data from the pig blood loss experiment:
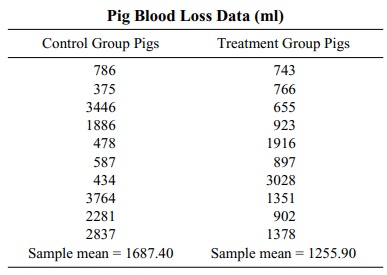
Do the results differ from the standard two-sample t test with pooled variance? Are the p-values similar?
14.2 Apply the Wilcoxon rank-sum test in the following
case to see if schizophrenia is randomly distributed across the seasons:
Season of Birth Among 100 Schizophrenic Patients

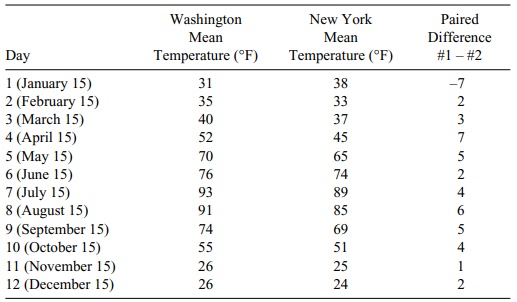
14.3 Using the following modification of the city data,
apply the Wilcoxon signed-rank test to determine whether there is a difference
in average tem-perature between the two cities. Compare your results to a
paired t test.
Daily Temperatures for Two Cities and Their Paired Differences
14.4 Apply the sign test to the above example. Did the
results change? Which test is more powerful, the sign test or the Wilcoxon
signed-rank test? Why?
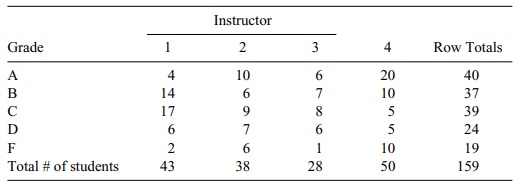
14.5 Suppose we compare four instructors for
consistency of grading. Use the following table to apply the Kruskal–Wallis
test to determine whether there is a difference among instructors.
Grade Counts for Students by Instructor
14.6 Based on the temperature data in Exercise 14.3,
use the day pairing to com-pute a Spearman rank order correlation between the
two cities.
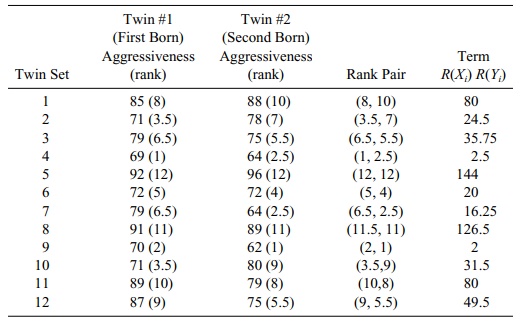
14.7 Use the modified aggressiveness scores for twins
(given in the table below) to apply the Wilcoxon signed-rank test. What is the p-value?
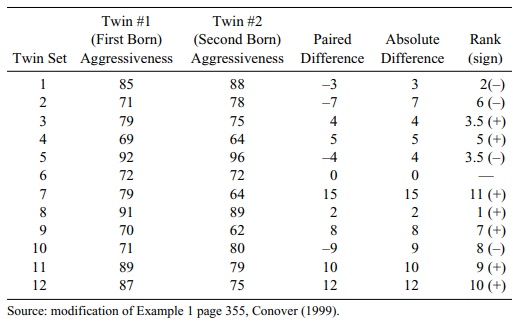
14.8 Apply the sign test to the data in Exercise 14.7.
Does the result change? What is the p-value?
14.9 Using the modified aggressiveness scores with the
aid of the table below, determine Spearman’s rank order correlation for the
twins.
Aggressiveness Scores for 12 Sets of Identical Twins
14.10 Recall the Lady Tasting Tea example. Suppose that
instead of being given four cups
with milk poured first and four cups with tea poured first, the lady was given
five cups with milk poured first and five cups with tea poured first. Suppose
the outcome of the experiment was as shown in the table at the top of the next
page.
Lady Tasting Tea Experiment:
Observed 2 × 2 Contingency Table for Fisher’s Exact Test
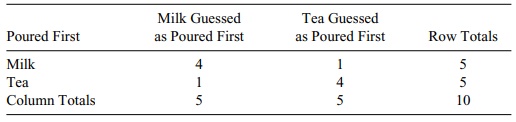
a. Determine the more extreme
tables.
b. Do a two-sided Fisher’s exact
test at the 0.05 level of the null hypothesis that the lady is guessing
randomly.
c. Do a one-sided test at the
0.05 level.
d. What is the p-value for the two-sided test?
e. What is the p-value for the one-sided test?
f. Which test makes more sense
here, one-sided or two-sided?
Answers:
14.1 First let us look at the two sample t test. The control group mean is 1687.4 and the treatment group mean is
1255.9. The pooled estimate of the standard deviation is 1073.075.
The t
statistic is (![]() c –
c – ![]() t)/(Sp √2/n), where n is the sample
size in each group. Since n = 10, Sp = 1073.75, and the mean
difference is 614.325, t = 0.8992.
This is not significant for a t with
18 degrees of freedom. Now consider the Wilcoxon test. We may see different
results because the distributions are very nonnormal. Consid-er the following
table:
t)/(Sp √2/n), where n is the sample
size in each group. Since n = 10, Sp = 1073.75, and the mean
difference is 614.325, t = 0.8992.
This is not significant for a t with
18 degrees of freedom. Now consider the Wilcoxon test. We may see different
results because the distributions are very nonnormal. Consid-er the following
table:
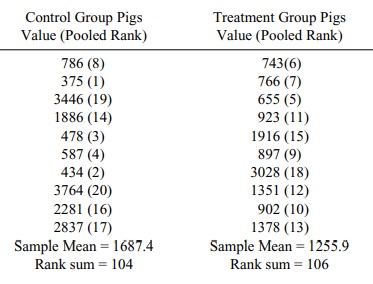
The rank sum for the first sample is 104 and the
rank sum for the control group and the treatment group is 106. They are
virtually the same. Both tests lead to the same conclusion. The two-sided p-value for the t test is close to 0.40. For the Wilcoxon test it is 0.97 for the
two-sided p-value and 0.38 for the t test (based on SAS results). The p-values are similar.
14.3 We consider the following table:
Daily Temperatures for Two Cities and Their Paired Differences
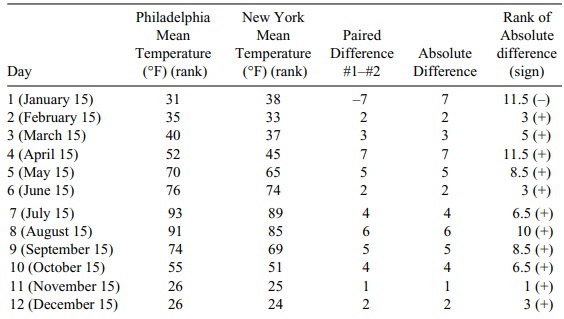
For the paired t
test, we have a mean difference of 2.833. The standard deviation of the
differences is S = 3.589 and the t statistic is t = 2.833/1.036 = 2.734. This is a Student t with 11 degrees of freedom under the null hypothesis. For a
two-sided 0.02 significance level, the critical t is 2.718. So since 2.734 > 2.718, the p-value is less than 0.02.
The sum of the negative ranks is only 11.5, whereas
the sum of the positive ranks is 66.5. If the null hypothesis were true, we
would expect these ranks to be approximately equal at around 39. The null
hypothesis is clearly rejected in this case. We get an approximate p-value by using the normal
approximation, Z = (11.5–39)/ √[(2n + 1)(39)/6], where n = 12 is the number of pairs. So Z = –27.5/ √[25(39)/6] = –27.5/12.75 = –2.157. This is a one-sided p-value of 0.5 – 0.4845 = 0.0155 or
two-sided p = 0.031. This agrees
closely with the result for the paired t
test.
14.9 We use the following table:
Aggressiveness Scores for 12 Identical Twins

Recall that the rank correlation is given by the
following formula:
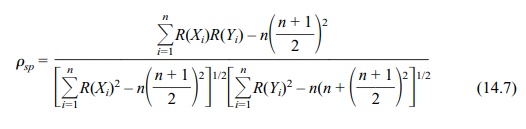
where n
is the number of ranked pairs, R(Xi) is the rank of Xi, and R(Yi) is the rank
of Yi.
The numerator is 612.5 – 12 (13/2)2 =
612.5 – 507 = 105.5. The terms in the denominator are (649 – 507)1/2
and (649 – 507)1/2. So ρsp = 105.5/(649 – 507) = 105.5/142 = 0.743 a strong positive relationship.
Related Topics
