Independent and Disjoint Events

INDEPENDENT AND DISJOINT EVENTS

Now we will give some formal definitions of independent events and disjoint events. But first we must explain the symbols for intersection and union of events.

Definition 5.3.1: Intersection. Let E and F be two events; then E ∩F denotes the event G that is the intersection of E and F. G is the collection of elementary events that are contained in both E and F.

We often say that G occurs only if both E and F occur. Let us define the union of two events.

Definition 5.3.2: Union. Let A and B be two events; then AU B denotes the event C that is the union of A and B. C is the collection of elementary events that are con-tained in both A and B or in either A or B.

In Example 2 (roll two dice independently), let E = {observe the same face on each die} and let F = {the first face is even}. Then E = [{1, 1}, {2, 2}, {3, 3}, {4, 4}, {5, 5}, and {6, 6}]. F = [{2, 1}, {2, 2}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {4, 1}, {4, 2}, {4, 3}, {4, 4}, {4, 5}, {4, 6}, {6, 1}, {6, 2}, {6, 3}, {6, 4}, {6, 5}, and {6, 6}]. Take G = E ∩ F. Because G consists of the common elementary events, G = [{2, 2}, {4, 4} and {6, 6}].

We see here that P(E) = 6/36 = 1/6, P(F) = 18/36 = 1/2, and P(G) = 3/36 = 1/12. When we intersect three or more events, for example, the events D, E, and F, we simply denote that intersection by K = D ∩ E ∩ F. This set is the same as taking the set H = D ∩ E and then taking K = H ∩ F, or taking G = E ∩ F and then finding K = D ∩G.

An additional point: The order in which the successive intersections is taken and the order in which the sets are arranged do not matter.

Definition 5.3.3: Mutual Independence. Let A₁, A₂, . . . , A_k be a set of k events (k is an integer greater than or equal to 2). Then these events are said to be mutually independent if P(A₁ ∩ A₂ ∩ . . . , A_k) = P(A₁)P(A₂) . . . P(A_k), and this equality of probability of intersection to product of individual probabilities must hold for any subset of these k events.

Definition 5.3.3 tells us that a set of events are mutually independent if, and only if, the probability of the intersection of any pair, or any set of three up to the set of all k events, is equal to the product of their individual probabilities. We will see shortly how this definition relates to our commonsense notion that independence means that one event does not affect the outcome of the others.

In Example 2, E and F are independent of each other. Remember that E = {observe the same face on each die} and F = {the first face is even}. We see from the commonsense notion that whether or not the first face is even has no effect on whether or not the second face will have the same number as the first.

We verify mutual independence from the formal definition by computing P(G) and comparing P(G) to P(E) P(F). We saw earlier that P(G) = 1/12, P(E) = 1/6, and P(F) = 1/2. Thus, P(E) P(F) = (1/6) (1/2) = 1/12. So we have verified that E and F are independent by checking the definition.

Now we will define mutually exclusive events.

Definition 5.3.4: Mutually Exclusive Events. Let A and B be two events. We say that A and B are mutually exclusive if A∩ B = Ø, or equivalently in terms of probabilites, if P(A∩ B) = 0. In particular, we note that A and A^c are mutually exclusive events.

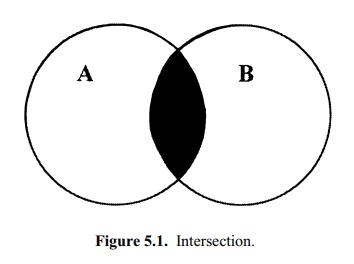
Figure 5.1. Intersection.

The distinction between the concepts of independent events and mutually exclu-sive events often leads to confusion. The two concepts are not related except that they both are defined in terms of probabilities of intersections.

Let us consider two nonempty events, A and B. Suppose A and B are indepen-dent. Now, P(A) > 0 and P(B) > 0, so P(A ∩ B) = P(A) P(B) > 0. Therefore, because P(A ∩ B) ≠ 0, A and B are not mutually exclusive.

Now consider two mutually exclusive events, C and D, which are also nonemp-ty. So P(C) > 0 and P(D) > 0, but P(C ∩ D) = 0 because C and D are mutually exclusive. Then, since P(C)P(D) > 0, P(C ∩ D) ≠ P(C)P(D); therefore, C and D are not independent.

Thus, we see that for two nonempty events, if the events are mutually exclusive, they cannot be independent. On the other hand, if they are independent, they cannot be mutually exclusive. Thus, these two concepts are in opposition.

Venn diagrams are graphics designed to portray combinations of sets such as those that represent unions and intersections. Figure 5.1 provides a Venn diagram for the intersection of events A and B.

Circles in the Venn diagram represent the individual events. In Figure 5.1, two circles, which represent events A and B, are labeled A and B. A third event, the in-tersection of the two events A and B, is indicated by the shaded area. Similarly, Fig-ure 5.2 provides a Venn diagram that illustrates the union of the same two events.

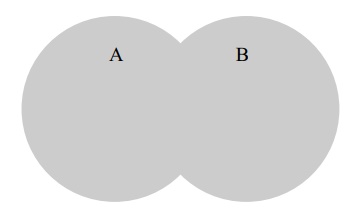
Figure 5.2. Union.

This illustration is accomplished by shading the regions covered by both of the indi-vidual sets in addition to the areas in which they overlap.