One-Compartment Open Model : Intravenous Bolus Administration

One-Compartment Open Model

Intravenous Bolus Administration

When a drug that distributes rapidly in the body is given in the form of a rapid intravenous injection (i.e. i.v. bolus or slug), it takes about one to three minutes for complete circulation and therefore the rate of absorption is neglected in calculations. The model can be depicted as follows:

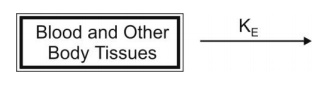
The general expression for rate of drug presentation to the body is:

dX/dt = Rate in (availability) - Rate out (elimination) (9.1)

Since rate in or absorption is absent, the equation becomes:

dX / dt = - Rate out (9.2)

If the rate out or elimination follows first-order kinetics, then:

dX/dt = K_Ε X (9.3)

where, K_E = first-order elimination rate constant, and

X = amount of drug in the body at any time t remaining to be eliminated.

Negative sign indicates that the drug is being lost from the body.

Estimation of Pharmacokinetic Parameters

For a drug that follows one-compartment kinetics and administered as rapid i.v. injection, the decline in plasma drug concentration is only due to elimination of drug from the body (and not due to distribution), the phase being called as elimination phase. Elimination phase can be characterized by 3 parameters—

1. Elimination rate constant

2. Elimination half-life

3. Clearance.

Elimination Rate Constant: Integration of equation 9.3 yields:

ln X = ln X_o – K_E t            (9.4)

where, X_o = amount of drug at time t = zero i.e. the initial amount of drug injected.

Equation 9.4 can also be written in the exponential form as:

X = X_o e^–KEt                                 (9.5)

The above equation shows that disposition of a drug that follows one-compartment kinetics is monoexponential.

Transforming equation 9.4 into common logarithms (log base 10), we get:

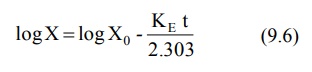
Since it is difficult to determine directly the amount of drug in the body X, advantage is taken of the fact that a constant relationship exists between drug concentration in plasma C (easily measurable) and X; thus:

X = V_d C                     (9.7)

where, V_d = proportionality constant popularly known as the apparent volume of distribution. It is a pharmacokinetic parameter that permits the use of plasma drug concentration in place of amount of drug in the body. The equation 9.6 therefore becomes:

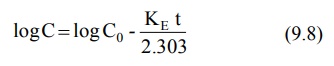
where, C_o = plasma drug concentration immediately after i.v. injection.

Equation 9.8 is that of a straight line and indicates that a semilogarithmic plot of log C versus t will be linear with Y-intercept log C_o. The elimination rate constant is directly obtained from the slope of the line (Fig. 9.2b). It has units of min^–1. Thus, a linear plot is easier to handle mathematically than a curve which in this case will be obtained from a plot of C versus t on regular (Cartesian) graph paper (Fig. 9.2a).

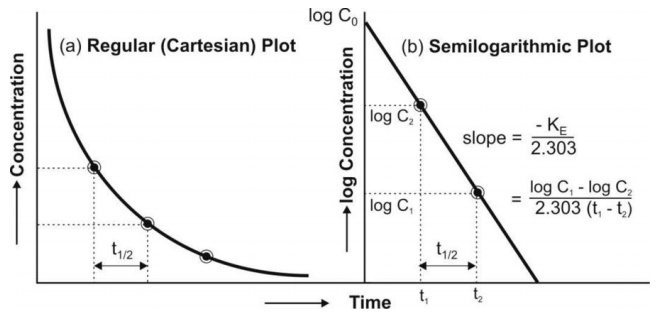
Fig. 9.2 (a) Cartesian plot of a drug that follows one-compartment kinetics and given by rapid i.v. injection, and (b) Semilogarithmic plot for the rate of elimination in a one-compartment model.

Thus, C_o, K_E (and t_½) can be readily obtained from log C versus t graph. The elimination or removal of the drug from the body is the sum of urinary excretion, metabolism, biliary excretion, pulmonary excretion, and other mechanisms involved therein. Thus, K_E is an additive property of rate constants for each of these processes and better called as overall elimination rate constant.

K_E = K_e + K_m + K_b + K_l + ...... (9.9)

The fraction of drug eliminated by a particular route can be evaluated if the number of rate constants involved and their values are known. For example, if a drug is eliminated by urinary excretion and metabolism only, then, the fraction of drug excreted unchanged in urine F_e and fraction of drug metabolized F_m can be given as:

Elimination Half-Life: Also called as biological half-life, it is the oldest and the best known of all pharmacokinetic parameters and was once considered as the most important characteristic of a drug. It is defined as the time taken for the amount of drug in the body as well as plasma concentration to decline by one-half or 50% its initial value. It is expressed in hours or minutes. Half-life is related to elimination rate constant by the following equation:

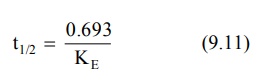
Elimination half-life can be readily obtained from the graph of log C versus t as shown in Fig 9.2.

Today, increased physiologic understanding of pharmacokinetics shows that half-life is a secondary parameter that depends upon the primary parameters clearance and apparent volume of distribution according to following equation:

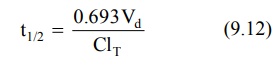
Apparent Volume of Distribution: The two separate and independent pharmacokinetic characteristics of a drug are –

1. Apparent volume of distribution, and

2. Clearance.

Since these parameters are closely related with the physiologic mechanisms in the body, they are called as primary parameters.

Modification of equation 9.7 defines apparent volume of distribution:

V_d is a measure of the extent of distribution of drug and is expressed in liters. The best and the simplest way of estimating V_d of a drug is administering it by rapid i.v. injection, determining the resulting plasma concentration immediately and using the following equation:

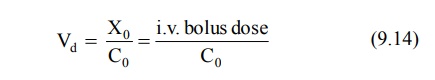
Equation 9.14 can only be used for drugs that obey one-compartment kinetics. This is because the V_d can only be estimated when distribution equilibrium is achieved between drug in plasma and that in tissues and such equilibrium is established instantaneously for a drug that follows one-compartment kinetics. A more general, more useful noncompartmental method that can be applied to many compartment models for estimating the V_d is:

For drugs given as i.v. bolus,

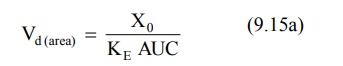
For drugs administered extravascularly (e.v.),

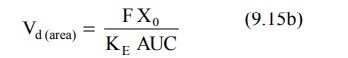
where, X_o = dose administered, and F = fraction of drug absorbed into the systemic circulation. F is equal to one i.e. complete availability when the drug is administered intravenously.

Clearance: Difficulties arise when one applies elimination rate constant and half-life as pharmacokinetic parameters in an anatomical/physiological context and as a measure of drug elimination mechanisms. A much more valuable alternative approach for such applications is use of clearance parameters to characterize drug disposition. Clearance is the most important parameter in clinical drug applications and is useful in evaluating the mechanism by which a drug is eliminated by the whole organism or by a particular organ.

Just as V_d is needed to relate plasma drug concentration with amount of drug in the body, clearance is a parameter to relate plasma drug concentration with the rate of drug elimination according to following equation:

Clearance is defined as the theoretical volume of body fluid containing drug (i.e. that fraction of apparent volume of distribution) from which the drug is completely removed in a given period of time. It is expressed in ml/min or liters/hour. Clearance is usually further defined as blood clearance (Cl_b), plasma clearance (Cl_p) or clearance based on unbound or free drug concentration (Cl_u) depending upon the concentration C measured for the right side of the equation 9.17.

Total Body Clearance: Elimination of a drug from the body involves processes occurring in kidney, liver, lungs and other eliminating organs. Clearance at an individual organ level is called as organ clearance. It can be estimated by dividing the rate of elimination by each organ with the concentration of drug presented to it. Thus,

The total body clearance, Cl_T, also called as total systemic clearance, is an additive property of individual organ clearances. Hence,

Total Systemic Clearance

Cl_T = Cl_R + Cl_H + Cl_Others (9.18d)

Because of the additivity of clearance, the relative contribution by any organ in eliminating a drug can be easily calculated. Clearance by all organs other than kidney is sometimes known as nonrenal clearance Cl_NR. It is the difference between total clearance and renal clearance.

According to an earlier definition (equation 9.17),

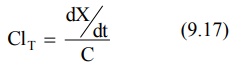
Substituting dX/dt = K_EX from equation 9.3 in above equation, we get:

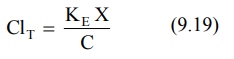
Since X/C = V_d (from equation 9.13), the equation 9.19 can be written as:

Cl_T = K _E V_d                  (9.20a)                          

Parallel equations can be written for renal and hepatic clearances as:

Cl_{R =} K _e V_d                   (9.20b)

Cl_{H =} K _m V_dm                   (9.20c)

Since K_E = 0.693/t_½ (from equation 9.11), clearance can be related to half-life by the following equation:

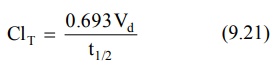
Identical equations can be written for Cl_R and Cl_H in which cases the t_½ will be urinary excretion half-life for unchanged drug and metabolism half-life respectively. Equation 9.21. shows that as Cl_T decreases, as in renal insufficiency, t_½ of the drug increases. As the Cl_T takes into account V_d, changes in V_d as in obesity or oedematous condition will reflect changes in Cl_T.

The noncompartmental method of computing total clearance for a drug that follows one-compartment kinetics is:

For a drug given by i.v. bolus, the renal clearance Cl_R may be estimated by determining the total amount of unchanged drug excreted in urine, X_u^∞ and AUC.

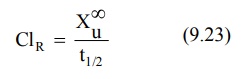
Organ Clearance: The best way of understanding clearance is at individual organ level. Such a physiologic approach is advantageous in predicting and evaluating the influence of pathology, blood flow, P-D binding, enzyme activity, etc. on drug elimination. At an organ level, the rate of elimination can be written as:

Substitution of equations 9.25 and 9.26 in equation 9.24 yields:

Rate of elimination = Q C_in - Q C_out

(also called as Rate of extraction) = Q (C_in - ^Cout ⁾ (9.27)

Division of above equation by concentration of drug that enters the organ of elimination C_in yields an expression for clearance of drug by the organ under consideration. Thus:

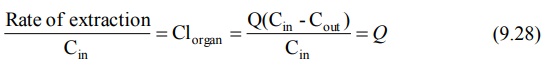
where, ER = (C_in – C_out)/C_in is called as extraction ratio. It has no units and its value ranges from zero (no elimination) to one (complete elimination). Based on ER values, drugs can be classified into 3 groups:

1. Drugs with high ER (above 0.7),

2. Drugs with intermediate ER (between 0.7 to 0.3), and

3. Drugs with low ER (below 0.3).

ER is an index of how efficiently the eliminating organ clears the blood flowing through it of drug. For example, an ER of 0.6 tells that 60% of the blood flowing through the organ will be completely cleared of drug. The fraction of drug that escapes removal by the organ is expressed as:

F=1-ER (9.29)

where, F = systemic availability when the eliminating organ is liver.

Hepatic Clearance: For certain drugs, the nonrenal clearance can be assumed as equal to hepatic clearance Cl_H. It is given as:

Cl_H  = Cl_T - Cl_R (9.30)

An equation parallel to equation 9.28 can also be written for hepatic clearance:

Cl_H = Q_H ER _H (9.31)

where,

Q_H = hepatic blood flow (about 1.5 liters/min), and

ER_H = hepatic extraction ratio.

The hepatic clearance of drugs can be divided into two groups:

1. Drugs with hepatic blood flow rate-limited clearance, and

2. Drugs with intrinsic capacity-limited clearance.

1. Hepatic Blood Flow: When ER_H is one, Cl_H approaches its maximum value i.e. hepatic blood flow. In such a situation, hepatic clearance is said to be perfusion rate-limited or flow-dependent. Alteration in hepatic blood flow significantly affects the elimination of drugs with high ER_H e.g. propranolol, lidocaine, etc. Such drugs are removed from the blood as rapidly as they are presented to the liver (high first-pass hepatic metabolism). Indocyanine green is so rapidly eliminated by the human liver that its clearance is often used as an indicator of hepatic blood flow rate. First-pass hepatic extraction is suspected when there is lack of unchanged drug in systemic circulation after oral administration. Maximum oral availability F for such drugs can be computed from equation 9.29. An extension of the same equation is the noncompartmental method of estimating F:

TABLE 9.1

Influence of Blood Flow Rate and Protein Binding on Total Clearance of Drugs with High and with Low ER Values

On the contrary, hepatic blood flow has very little or no effect on drugs with low ER_H e.g. theophylline. For such drugs, whatever concentration of drug present in the blood perfuses liver, is more than what the liver can eliminate (low first-pass hepatic metabolism). Similar discussion can be extended to the influence of blood flow on renal clearance of drugs. This is illustrated in Table 9.1. Hepatic clearance of a drug with high ER is independent of protein binding.

2. Intrinsic Capacity Clearance: Denoted as Cl_int, it is defined as the inherent ability of an organ to irreversibly remove a drug in the absence of any flow limitation. It depends, in this case, upon the hepatic enzyme activity. Drugs with low ER_H and with elimination primarily by metabolism are greatly affected by changes in enzyme activity. Hepatic clearance of such drugs is said to be capacity-limited, e.g. theophylline. The t_½ of such drugs show great intersubject variability. Hepatic clearance of drugs with low ER is independent of blood flow rate but sensitive to changes in protein binding.

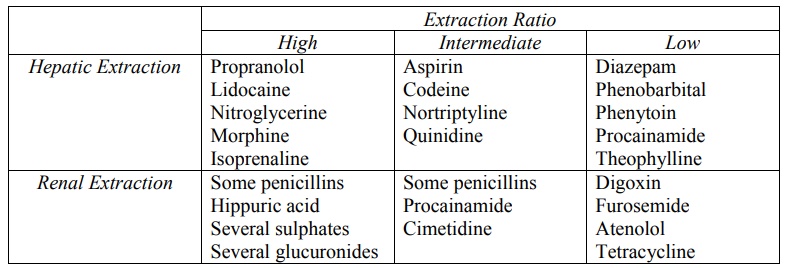
The hepatic and renal extraction ratios of some drugs and metabolites are given in Table 9.2.

TABLE 9.2

Hepatic and Renal Extraction Ratio of Some Drugs and Metabolites