One-Compartment Open Model: Extravascular Administration
| Home | | Biopharmaceutics and Pharmacokinetics |Chapter: Biopharmaceutics and Pharmacokinetics : Compartment Modelling
a. Zero-Order Absorption Model b. First-Order Absorption Model
One-Compartment Open Model
Extravascular Administration
When a drug is administered by extravascular route
(e.g. oral, i.m., rectal, etc.), absorption is a prerequisite for its
therapeutic activity. Factors that influence drug absorption have already been
discussed in chapter 2. The rate of
absorption may be described mathematically as a zero-order or first-order
process. A large number of plasma concentration-time profiles can be described
by a one-compartment model with first-order absorption and elimination.
However, under certain conditions, the absorption of some drugs may be better
described by assuming zero-order (constant rate) kinetics. Differences between
zero-order and first-order kinetics are illustrated in Fig. 9.6.
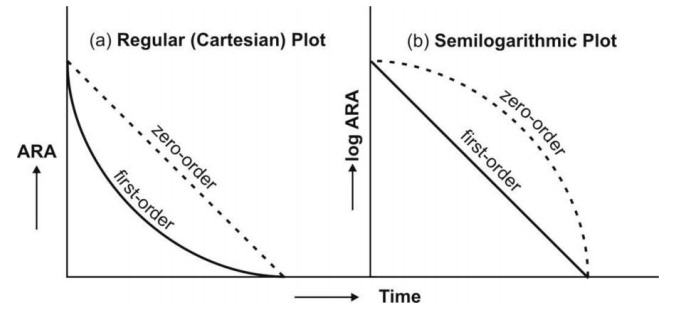
Fig. 9.6 Distinction between zero-order and first-order absorption processes.
Figure a is regular plot, and Figure b a semilog plot of amount of drug
remaining to be absorbed (ARA) versus time t.
Zero-order absorption is characterized by a constant rate of absorption. It is independent of amount
remaining to be absorbed (ARA), and its regular ARA versus t plot is linear
with slope equal to rate of absorption while the semilog plot is described by
an ever-increasing gradient with time. In contrast, the first-order absorption
process is distinguished by a decline in the rate with ARA i.e. absorption rate
is dependent upon ARA; its regular plot is curvilinear and semilog plot a
straight line with absorption rate constant as its slope.
After e.v. administration, the rate of change in
the amount of drug in the body dX/dt is the difference between the rate of
input (absorption) dXev/dt and rate of output (elimination) dXE/dt.
dX/dt = Rate of absorption – Rate of elimination
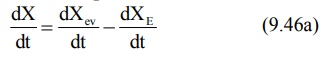
For a drug that follows one-compartment kinetics,
the plasma concentration-time profile is characterized by absorption phase,
post-absorption phase and elimination phase (Fig. 9.7.).
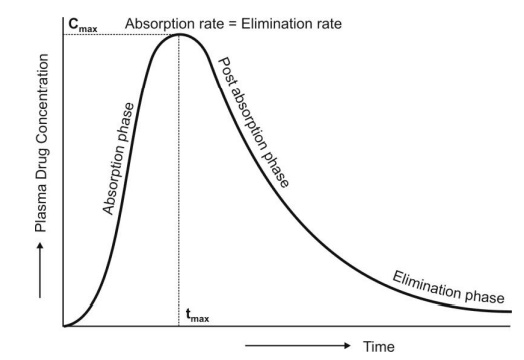
Fig. 9.7 The absorption and elimination
phases of the plasma concentration-time profile obtained after extravascular administration of a single dose of a
drug.
During the absorption
phase, the rate of absorption is greater than the rate of elimination
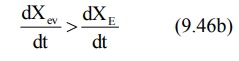
At peak plasma concentration, the rate of
absorption equals the rate of elimination and the change in amount of drug in
the body is zero.
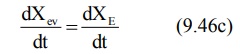
During the post-absorption
phase, there is some drug at the extravascular site still remaining to be
absorbed and the rate of elimination at this stage is greater than the
absorption rate.
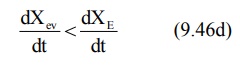
After completion of drug absorption, its rate
becomes zero and the plasma level time curve is characterized only by the elimination phase.
a. Zero-Order Absorption Model
This model is similar to that for constant rate
infusion.

The rate of drug absorption, as in the case of
several controlled drug delivery systems, is constant and continues until the
amount of drug at the absorption site (e.g. GIT) is depleted. All equations
that explain the plasma concentration-time profile for constant rate i.v.
infusion are also applicable to this model.
b. First-Order Absorption Model
For a drug that enters the body by a first-order
absorption process, gets distributed in the body according to one-compartment
kinetics and is eliminated by a first-order process, the model can be depicted
as follows:

The differential form of the equation 9.46a is:
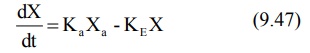
where,
Ka = first-order absorption rate
constant, and
Xa = amount of drug at the absorption
site remaining to be absorbed i.e. ARA.
Integration of equation 9.47 yields:
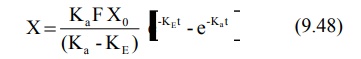
Transforming into concentration terms, the equation
becomes:
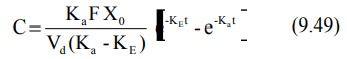
where F = fraction of drug absorbed systemically
after e.v. administration. A typical plasma concentration-time profile of a
drug administered e.v. is shown in Fig. 9.7.
Assessment of Pharmacokinetic Parameters
Cmax and tmax: At peak
plasma concentration, the rate of absorption equals rate of elimination i.e. KaXa = KEX and
the rate of change in plasma drug concentration dC/dt = zero. This rate can be
obtained by differentiating equation 9.49.
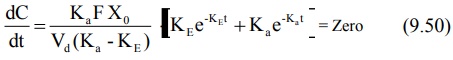
On simplifying, the above equation becomes:

Converting to logarithmic form,
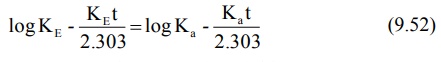
where t is tmax. Rearrangement of above
equation yields:
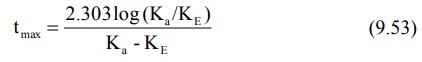
The above equation shows that as Ka becomes
larger than KE, tmax becomes smaller since (Ka
– KE) increases much faster than log Ka/KE. Cmax
can be obtained by substituting equation 9.53 in equation 9.49. However, a
simpler expression for the same is:
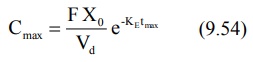
It has been shown that at Cmax, when Ka
= KE, tmax = 1/KE. Hence, the above equation
further reduces to:
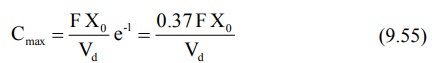
Since FXo/Vd represents Co
following i.v. bolus, the maximum plasma concentration that can be attained
after e.v. administration is just 37% of the maximum level attainable with i.v.
bolus in the same dose. If bioavailability is less than 100%, still lower
concentration will be attained.
Elimination Rate Constant: This
parameter can be computed from the elimination phase of the plasma level time profile. For most drugs administered
e.v., absorption rate is significantly greater than the elimination rate i.e. Kat
>> KEt. Hence, one can say that e–Kat approaches
zero much faster than does e–KEt. At such a stage, when absorption
is complete, the change in plasma concentration is dependent only on
elimination rate and equation 9.49 reduces to:
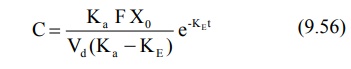
Transforming into log form, the equation becomes:
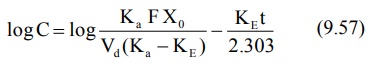
A plot of log C versus t yields a straight line
with slope –KE/2.303 (half-life can then be computed from KE).
KE can also be estimated from urinary excretion data (see the section on urinary excretion data).
Absorption Rate Constant: It can be
calculated by the method of residuals.
The technique is also known as feathering, peeling and stripping.
It is commonly used in pharmacokinetics to resolve a multiexponential curve
into its individual components. For a drug that follows one-compartment
kinetics and administered e.v., the concentration of drug in plasma is
expressed by a biexponential equation 9.49.
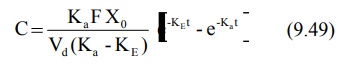
If KaFXo/Vd(Ka-KE)
= A, a hybrid constant, then:
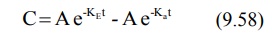
During the elimination phase, when absorption is
almost over, Ka >> KE and the value of second
exponential e–Kat approaches zero whereas the first exponential e–KEt
retains some finite value. At this time, the equation 9.58 reduces to:
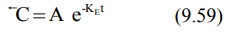
In log form, the above equation is:
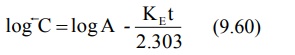
where C represents the back extrapolated plasma
concentration values. A plot of log C versus t yields a biexponential curve
with a terminal linear phase having slope –KE/2.303 (Fig. 9.8). Back
extrapolation of this straight line to time zero yields y-intercept equal to
log A.
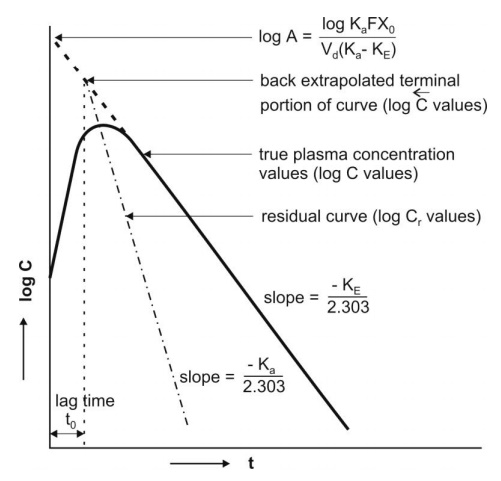
Fig. 9.8 Plasma concentration-time profile after oral administration of a single
dose of a drug. The biexponential
curve has been resolved into its two components— absorption and elimination.
Subtraction of true plasma concentration values
i.e. equation 9.58 from the extrapolated plasma concentration values i.e.
equation 9.59 yields a series of residual concentration values Cr :
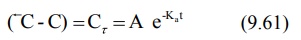
In log form, the equation is:
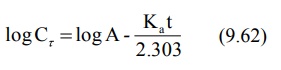
A plot of log Cr versus t yields a
straight line with slope –Ka/2.303 and Y-intercept log A (Fig. 9.8). Absorption half-life can then be
computed from Ka using the relation 0.693/Ka.
Thus, the method of residuals enables resolution of
the biexponential plasma level-time curve into its two exponential components.
The technique works best when the difference between Ka and KE
is large (Ka/KE ≥ 3). In
some instances, the KE obtained after i.v. bolus of the same drug is
very large, much larger than the Ka obtained by the method of
residuals (e.g. isoprenaline) and if KE/Ka ≥ 3, the terminal slope estimates Ka and not KE
whereas the slope of residual line gives KE and not Ka.
This is called as flip-flop phenomenon since the slopes of the two lines have exchanged their
meanings.
Ideally, the extrapolated and the residual lines
intersect each other on y-axis i.e. at time t = zero and there is no lag in
absorption. However, if such an intersection occurs at a time greater than
zero, it indicates time lag. It is defined as the time difference between
drug administration and start of
absorption. It is denoted by symbol to and represents the beginning
of absorption process. Lag time should not be confused with onset time.
The above method for the estimation of Ka
is a curve-fitting method. The
method is best suited for drugs which are rapidly and completely absorbed and
follow one-compartment kinetics even when given i.v. However, if the absorption
of the drug is affected in some way such as GI motility or enzymatic
degradation and if the drug shows multicompartment characteristics after i.v.
administration (which is true for virtually all drugs), then Ka computed
by curve-fitting method is incorrect even if the drug were truly absorbed by
first-order kinetics. The Ka so obtained is at best, estimate of
first-order disappearance of drug from the GIT rather than of
first-order appearance in the systemic circulation.
Wagner-Nelson Method for Estimation of Ka
One of the better alternatives to curve-fitting
method in the estimation of Ka is Wagner-Nelson method. The method
involves determination of Ka from percent unabsorbed-time plots and
does not require the assumption of zero- or first-order absorption.
After oral administration of a single dose of a
drug, at any given time, the amount of drug absorbed into the systemic
circulation XA, is the sum of amount of drug in the body X and the
amount of drug eliminated from the body XE. Thus:
XA = X + XE (9.63)
The amount of drug in the body is X = VdC.
The amount of drug eliminated at any time t can be calculated as follows:
XE = KEVd [AUC] 0t
(9.64)
Substitution of values of X and XE in
equation 9.63 yields:
XA = VdC + KEVd
[AUC]0t (9.65)
The total amount of drug absorbed into the systemic
circulation from time zero to infinity XA∞ can be given as:
XA∞ = Vd C∞ + KE Vd
[AUC]∞0 (9.66)
Since at t = ∞, C∞ = 0, the above equation reduces to:
X∞A = KE
Vd [AUC] ∞0 (9.67)
The fraction of drug absorbed at any time t is
given as:
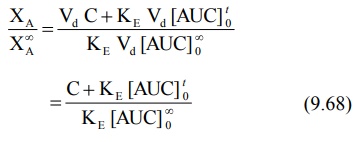
Percent drug unabsorbed at any time is therefore:
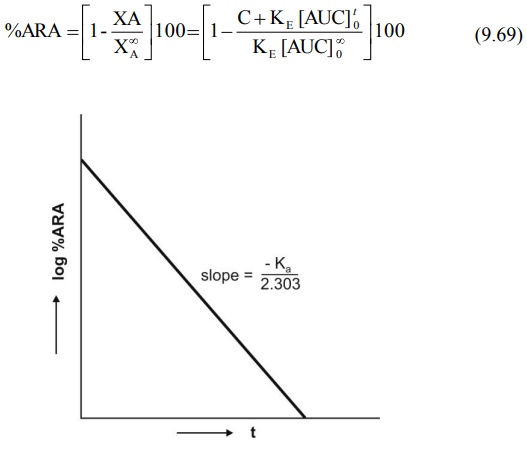
Fig. 9.9 Semilog plot of percent ARA
versus t according to Wagner-Nelson method.
Similar plot is obtained for Loo-Reigelman method
The method requires collection of blood samples
after a single oral dose at regular intervals of time till the entire amount of
drug is eliminated from the body. KE is obtained from log C versus t
plot and [AUC]ot and [AUC] ∞o are obtained from plots of C versus t. A semilog plot of percent
unabsorbed (i.e. percent ARA) versus t yields a straight line whose slope is –Ka/2.303
(Fig.9.9). If a regular plot of the same is a straight line, then absorption is
zero-order.
Ka can similarly be estimated from
urinary excretion data (see the relevant
section). The biggest disadvantage
of Wagner-Nelson method is that it applies only to drugs with one-compartment
characteristics. Problem arises when a drug that obeys one-compartment model
after e.v. administration shows multicompartment characteristics on i.v.
injection.
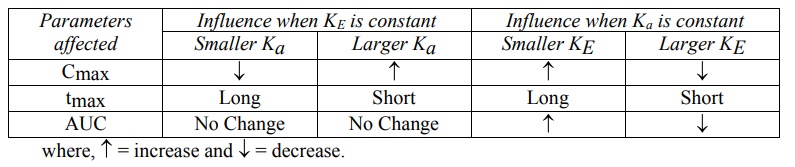
Effect of Ka and KE on Cmax, tmax and AUC
A summary of the influence of changes in Ka
at constant KE and of KE at constant Ka on Cmax,
tmax and AUC of a drug administered e.v. is shown in Table 9.4.
TABLE 9.4
Influence of Ka and KE on Cmax, tmax
and AUC
Apparent Volume of Distribution and Clearance: For a drug that follows one-compartment kinetics after e.v.
administration, Vd and ClT can be computed from equation
9.15b and 9.22b respectively where F is the fraction absorbed into the systemic
circulation.
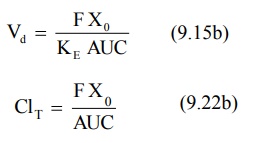
Related Topics