Two-Compartment Open Model: Extravascular Administration - First-Order Absorption

Two-Compartment Open Model

Extravascular Administration – First-Order Absorption

The model can be depicted as follows:

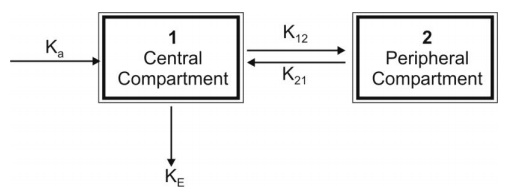
For a drug that enters the body by a first-order absorption process and distributed according to two-compartment model, the rate of change in drug concentration in the central compartment is described by 3 exponents —an absorption exponent, and the two usual exponents that describe drug disposition.

The plasma concentration at any time t is given by equation:

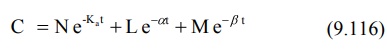
C = Absorption exponent + Distribution exponent + Elimination exponent

where Ka, α and β have usual meanings. L, M and N are coefficients.

The 3 exponents can be resolved by stepwise application of method of residuals assuming Ka > α > β as shown in Fig. 9.14. The various pharmacokinetic parameters can then be estimated.

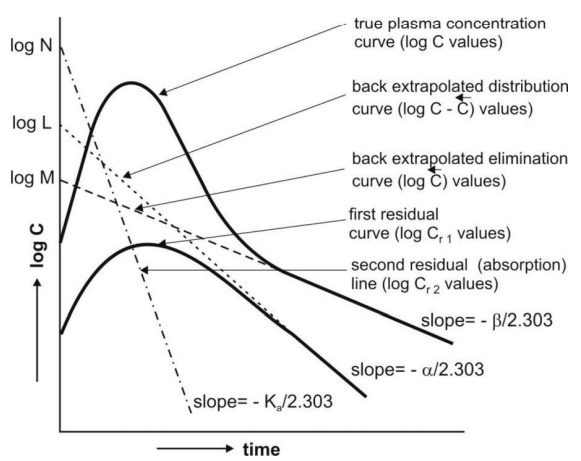
Fig. 9.14. Semilog plot of C versus t of a drug with two-compartment characteristics when administered extravascularly. The various exponents have been resolved by the method of residuals.

Besides the method of residuals, K_a can also be estimated by Loo-Riegelman method for a drug that follows two-compartment characteristics. This method is in contrast to the Wagner-Nelson method for determination of K_a of a drug with one-compartment characteristics. The Loo-Riegelman method requires plasma drug concentration-time data both after oral and i.v. administration of the drug to the same subject at different times in order to obtain all the necessary kinetic constants. Despite its complexity, the method can be applied to drugs that distribute in any number of compartments.