Sampling: Probability Profile

SAMPLING : PROBABILITY PROFILE

Sampling refers to - ‘the process of selecting a portion or part to represent the whole’.

In usual practice, a ‘sterility test’ attempts to infer and ascertain the state (sterile or non-sterile) of a particular batch ; and, therefore, it designates predominantly a ‘statistical operation’.

Let us consider that ‘p’ duly refers to the proportion of infected containers in a batch, and ‘q’ the proportion of corresponding non-infected containers. Then, we may have :

p + q = 1

or q = 1 – p

Further, we may assume that a specific ‘sample’ comprising of two items is duly withdrawn from a relatively large batch containing 10% infected containers. Thus, the probability of a single item taken at random contracting infection is usually given by the following expression :

p = 0.1         [i.e., 10% = 0.1]

whereas, the probability of such an item being non-infected is invariably represented by the following expression :

q = 1 – p = 1 – 0.1 = 0.9

Probability Status—The probability status of the said two items may be obtained virtually in three different forms, such as :

(a) When both items get infected : p² = 0.01

(b) When both items being non-infected : q² = (1 – p)² = (0.9)² = 0.81, and

(c) When one item gets infected and the other one non-infected : 1 – (p² + q²)

or = 1 – (0.01 + 0.81) = 1 – (0.82)

or = 0.18

i.e., = 2pq

Assumption : In a particular ‘sterility test’ having a ‘sample’ size of ‘n’ containers, the ensuing probability p of duly accomplishing ‘n’ consecutive ‘steriles’ is represented by the following expres-sion :

qⁿ = (1 – p)ⁿ

Consequently, the ensuing values for various levels of ‘p’* having essentially a constant sample size are as provided in the following. Table 8 : 4A, that evidently illustrates that the ‘sterility test’ fails to detect rather low levels of contamination contracted/present in the ‘sample’.

Likewise, in a situation whereby different sample sizes were actually used**, it may be em-phatically demonstrated that as the sample size enhances, the probability component of the batch being passed as sterile also gets decreased accordingly.

Table 8.4 : Sampling in Sterility Testing

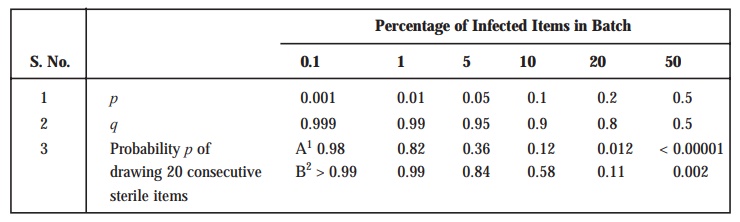
1. A : First Sterility Test : Calculated from P = (1 – p)²⁰ = q²⁰

2. B : First Re-Test : Calculated from P = (1 – p)²⁰ [2 – (1 – p)²⁰]

[Adapted From : Hugo and Russell : Pharmaceutical Microbiology, PG Publishing Pvt. Ltd., New Delhi, 3rd edn., 1984]

In actual practice, however, the additional tests, recommended by BP (1980), enhances substan-tially the very chances of passing a specific batch essentially comprising of a proportion or part of the infected items (see Table : 8.4B). Nevertheless, it may be safely deduced by making use of the following mathematical formula :

(1 – p)ⁿ [2 – (1 – p)ⁿ]

that provides adequate chance in the ‘First Re-Test’ of passing a batch comprising of a proportion or part ‘p’ of the infected containers.