Binary Mixtures of Miscible Liquids

Binary Mixtures of Miscible Liquids

The Relation of Vapor Pressure and Mixture Composition

When the two components of a binary mixture are completely miscible, the vapor pressure of a mixture is a function of mixture composition as well as the vapor pressures of the two pure components. If the liquids are ideal, the relation of vapor pressure and composition is given by Raoult’s law. At a constant temperature, the partial vapor pressure of a constituent of an ideal mixture is proportional to its mole fraction in the liquid. Thus, for a mixture of A and B,

P_A = P_A^o X_A                  (10:7)

where P_A is the partial vapor pressure of A in the mixture, P_A^o is the vapor pressure of pure A, and x_A is its mole fraction. Similarly,

P_B = P_B^oX_B                    (10:8)

The total pressure of the system, P, is simply P_A + P_B.

These relations can be expressed graphically. If the vapor pressure at a given temperature of each pure component is marked on a graph of vapor pressure versus mole fraction, the total vapor pressure at the same temperature of a liquid mixture of any composition falls on the straight line joining the vapor pressures of the two components. The partial pressure of each component is indicated by the diagonals of this figure. The principle is shown in Figure 10.4. A separate relation must be constructed for each temperature.

Very few liquid mixtures rigidly obey Raoult’s law. Consequently, the vapor pressure data must be determined experimentally. Mixtures that deviate positively from the law give a total vapor pressure curve that lies above the theoretical straight line. Negative deviations fall below the line. In extreme cases, deviations are so large that a range of mixtures will exhibit a higher or lower vapor pressure than that of either of the pure components.

Returning to ideal systems, the partial pressure of a component in the vapor is proportional to its mole fraction. For component A,

P_A = y_AP                 (10:9)

where P_A is the partial pressure of A in the vapor and y_A is its mole fraction.

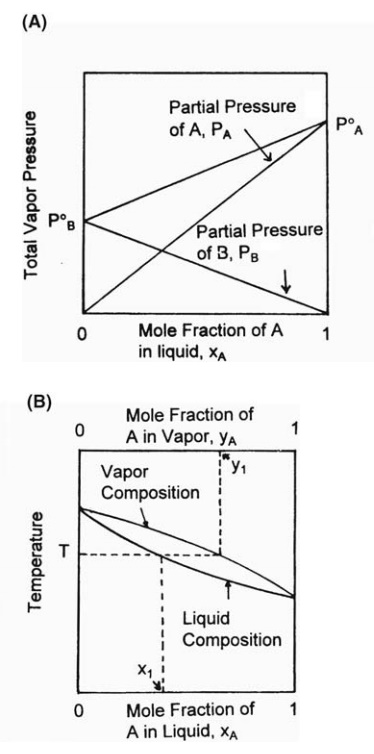
FIGURE 10.4 (A) The vapor pressure of an ideal binary mixture. (B) Phase diagram.

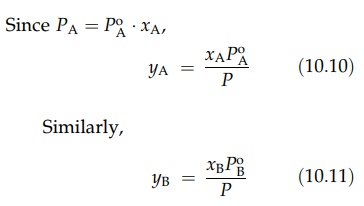
If A is the more volatile component, P_A^o is greater than P · y_A is therefore greater than x_A, that is, the vapor is richer in the more volatile component than the liquid with which it is in equilibrium.

The Relation of Boiling Point and Mixture Composition

For the purposes of distillation, curves relating vapor pressure and composition are usually replaced by boiling point curves. These are determined by experi-ment at the given pressure. Figure 10.5A represents a system in which the vapor pressure of some mixtures is greater than the vapor pressure of the pure, more volatile component. This system will exhibit a minimum boiling point, and the composition of the liquid at this point is given by Z. This mixture, which is a constant-boiling or azeotropic mixture, evolves on boiling a vapor of the same composition. In the binary system described in Figure 10.5B, mixtures are formed with a vapor pressure that is less than that of the less volatile compo-nent. The maximum boiling point is given by the azeotropic mixture, Z.

Systems that form minimum-boiling mixtures are common. Ethyl alcohol and water provide an example, the azeotrope containing 4.5% by weight of water. The boiling point at atmospheric pressure is 351.15 K, 0.25 K lower than the boiling point of pure alcohol. Maximum-boiling mixtures are less common. The most familiar example is hydrochloric acid, which forms an azeotrope boiling at 381 K and contains 20.2% by weight of hydrochloric acid.

Mixtures that form azeotropes cannot be separated into the pure compo-nents by normal distillation methods. However, separation into the azeotrope and one pure component is possible. Efficient fractionation of the mixture M of Figure 10.5A would give the azeotrope Z as distillate and pure B as the residue.

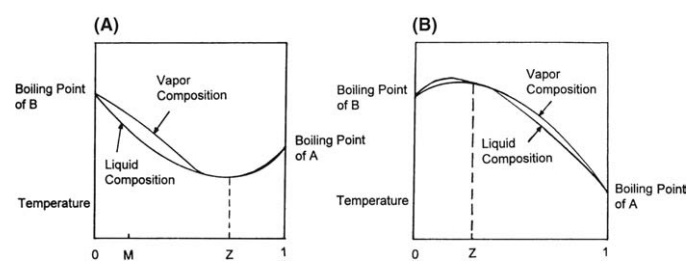
FIGURE 10.5 Temperature-composition diagrams for a binary mixture. (A) Minimum azeotrope and (B) maximum azeotrope.

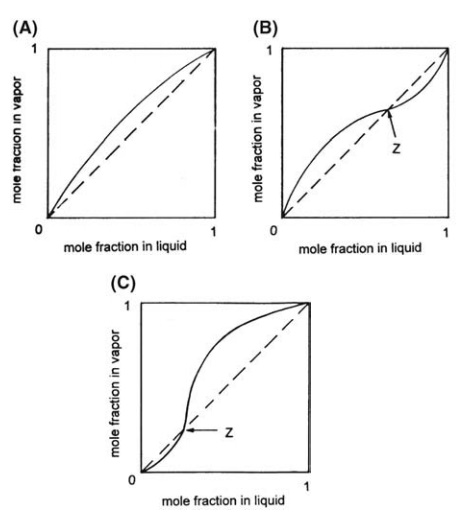
FIGURE 10.6 Vapor-liquid equilibrium diagrams.

The composition of the azeotropic mixture of a system is a function of the total pressure, and it is possible, in some cases, to eliminate the constant-boiling mixture by altering the pressure at which the distillation is performed. For example, at pressures less than 100 mmHg, ethyl alcohol and water do not form an azeotrope. At this pressure, they can be completely separated.

Vapor-Liquid Equilibrium Diagrams

Vapor-liquid equilibrium diagrams of the form shown in Figure 10.6 provide an alternative and convenient method of recording distillation data. They consist of a conventional graph relating the mole fraction of the more volatile component in the liquid, designated X, to the mole fraction of the more volatile component in the vapor, designated Y. An ideal binary system is shown in Figure 10.6A. The temperature varies along each of the curves, and the diagram is only applicable to the pressure at which the variables were measured. Curves of min-imum-boiling mixtures and maximum-boiling mixtures are drawn in Figure 10.6B and C, respectively.

Simple or Differential Distillation

In simple or differential distillation, the vapor evolved from the boiling mixture is immediately removed and condensed. For the system shown in Figure 10.7A, the liquid of composition x₁ evolves a vapor of composition y₁. Its removal impoverishes the liquid in the more volatile component. The composition of the liquid moves toward pure B, and its boiling point increases. There is, therefore, a progressive change in the composition of the vapor, the mole fraction of the more volatile component steadily decreasing. Unless the boiling points of the two pure components differ widely, a reasonable degree of separation is not possible. The method may be used to remove low–boiling point solvents from aqueous solutions.