Evaporation

EVAPORATION

Evaporation may be defined as the removal of a solvent from a solution by vaporization but is usually restricted to the concentration of solutions by boiling. Crystallization and drying, which may also utilize the vaporization of a liquid, are considered in subsequent sections.

Evaporation in the pharmaceutical industry is primarily associated with the removal by boiling of water and other solvents in batch processes. However, the principles that govern such processes apply more generally and are derived from a study of the transfer of heat to the boiling liquid, the relevant physical properties of the liquid, and the thermal stability of its components.

Heat Transfer to Boiling Liquids in an Evaporator

The heat required to boil a liquid in an evaporator is usually transferred from a heating fluid, such as steam or hot water, across the wall of a jacket or tube in or around which the liquid boils. A qualitative discussion of the methods used to secure high rates of heat flow can be based on equation (3.9):

 Q = UAΔT

where Q is the rate of heat flow, U is the overall heat transfer coefficient, A is the area over which heat is transferred, and ΔT is the difference in temperature between the fluids.

The overall heat transfer coefficient is derived from a series of individual coefficients that characterize the thermal barriers that oppose heat transfer. Thus, for the heating fluid, the film coefficient for a condensing vapor, such as steam, is high provided permanent gases and condensate are removed by venting and draining. With liquid heating media, the velocity of flow over the heat transfer surface should be as high as is practicable. If the solid barrier consists of a thin metal wall, the resistance to heat flow will be small. Resistance, however, is significantly increased by chemical scale, which may be deposited on either side. The accumulation of scale should be prevented. A glass wall may provide the largest thermal resistance of the system. Neglecting the thermal stability of the boiling liquid, circulation of the liquid should be rapid and, because of its influence on viscosity, the temperature of boiling should be as high as possible. Both factors promote high film coefficients on the product side of the wall.

Other factors described by the above equation are the area of the heat transfer surfaces, which should be as large as possible, and the temperature difference between the heating surface and the boiling liquid. As long as the critical heat flux is not exceeded, the latter should also be large.

The Physical Properties of Solution and Liquids

A number of physical factors, which are interrelated in a complex way, are relevant to a study of evaporation. For a given heating fluid, the temperature difference across the wall of an evaporator is determined by the temperature of boiling, a variable controlled by the external pressure and the concentration of the solute in the solution. Both the boiling temperature and the solute concen-tration influence the viscosity of the solution, a factor that greatly affects the heat transfer coefficient. The temperature of boiling also determines the solubility of dissolved constituents and the degree of concentration that can be carried out without separation of solids.

The Relation Between Boiling Temperature and Solute Concentration

When a solute is dissolved in a solvent, the vapor pressure is depressed and the boiling point rises. Since the boiling point increases as the solute concentration increases, the temperature difference between the boiling liquid and the heating surface falls. For dilute solutions, the expected rise in boiling point can be cal-culated from Raoult’s law. However, this procedure is not applicable to con-centrated solutions or to solutions of uncertain composition. For aqueous, concentrated solutions, Duhring’s rule may be used to obtain the boiling point rise of a solution at any pressure. This rule states that the boiling point of a given solution is a linear function of the boiling point of water at the same pressure. A family of lines is required to cover a range of concentration, as shown in Figure 10.1.

The Relation of Boiling Temperature and External Pressure

The temperature at which a solution of given composition boils is determined by the external pressure. The vapor pressure of a pure solvent at any temperature can usually be obtained from published tables. Alternatively, if the vapor pressure at two temperatures is known, the plot of the logarithm of the vapor pressure against the reciprocal of the absolute temperature yields an approxi-mately straight line. For intermediate pressures, the temperature at which the solvent will boil can be found by interpolation. If dissolved substances are present, the boiling point must be adjusted using Duhring’s rule. This value permits an accurate estimate of the temperature differences in the evaporator.

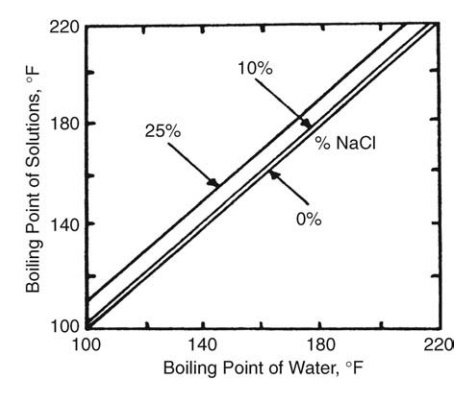
FIGURE 10.1 Duhring’s chart for sodium chloride.

Reduction in the external pressure lowers the boiling temperature and, if the associated increase in viscosity is not too great, increases the rate of evap-oration. On large installations, a moderate vacuum is widely used to increase the capacity of an evaporator. The imposition of low pressures and low boiling temperatures is also necessary when thermolabile materials are processed.

Boiling in tubes is commonly used in evaporators. In these circumstances, the hydrostatic head developed by a column of liquid or the friction head imposed by its movement can create a local increase in pressure, which sup-presses boiling and decreases the evaporating capacity of the system.

The Relation of Viscosity with Temperature and Solute Concentration

The viscosity of a solution is modified by changes in temperature and solute concentration. Since a low viscosity promotes a high heat transfer coefficient, the exponential decrease of viscosity with increase in temperature is of great importance and indicates a high boiling temperature.

In general, the addition of a nonvolatile solute increases the viscosity of a solution at any temperature. Consequently, the viscosity of the solution increases as the evaporation proceeds. These effects, however, cannot be calculated.

If at the operating temperatures and concentrations, the viscosity of a solution is high, satisfactory heat transfer coefficients may only be obtained if the liquid is driven over the heating surface. In other systems, movement of a viscous liquid is assisted by gravity or the liquid in contact with the heating surface is disrupted mechanically by scrapers.

The Effect of Temperature on Solubility

The solubility of the components of a solution depends on the temperature. Most commonly, solubility increases with increase in temperature, so a greater degree of concentration is possible at higher temperatures without the separa-tion of solids. The reverse is true for liquids containing scale-forming solids with inverse solubility characteristics, such as calcium or magnesium sulfate, or materials that decompose and deposit, such as coagulable protein.

The Effect of Heat on the Active Constituents of a Solution

The thermal stability of components of a solution may determine the type of evaporator to be used and the conditions of its operation. If a simple solution contains a hydrolyzable material and the rate of its degradation during evaporation depends on its concentration at any time, an exponential relation between the remaining fraction, F, and the time, t, characteristic of a first-order reaction, is obtained:

F = e^-kt                    (10:1)

The dependence of the reaction velocity constant, k, on the absolute tem-perature, T, is expressed by the relation

k = Ae^-(B/T)                          (10:2)

where A and B are constants characteristic of the reaction. Thus, at temperatures T₁, T₂, and T₃, where T₁ > T₂ > T₃, the relation between remaining fraction and time of heating shown in Figure 10.2 emerges. This indicates the importance of

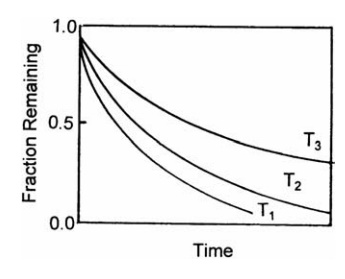
FIGURE 10.2 The effect of time and temper-ature on degradation.

the temperature and time of heating. If the latter can be shortened, the temperature of evaporation can be greatly increased without increasing the fraction that is degraded. If, therefore, the effect of temperature on the rate of evaporation is known, it is possible to define conditions of time and temperature at which decomposition is a minimum.

In practice, the kinetics of degradation and the relation of evaporation rate and temperature are usually not known. This is particularly true when the criteria by which the product is judged are color, taste, and smell. In addition, the analysis above neglects temperature variation in the evaporating liquid and degradation in boundary films where temperatures are higher. Often, therefore, experiments are necessary to determine the suitability of an evaporation process.

In batch processes, the time of exposure to heat is well defined. This is also true for continuous processes in which the liquid to be evaporated is passed only once through the heater. In continuous processes in which the liquid is recirculated through the heater, the average residence time, a, is given by the ratio

Working volume of evaporato / Volumetric discharge

in which volumetric discharge is only an indication of the damage that prolonged heating may cause. If perfect mixing occurs in the evaporator, the fraction, f, which is in the unit for time, t, or less is given by the equation

_{f = 1- e}^-(t/a)           (10:3)

This relation shows, for example, that an evaporator with an average residence time of one hour holds 13.5% of active principles for two hours and about 2% for four hours.