Factorial Design

FACTORIAL DESIGN

The effects of a number of different factors are explored simultaneously in factorial designs. The treatment consists of all combinations that can be formed from the different factors. The simplest case is one in which each factor is considered at two levels. This is described as a 2ⁿ factorial design. For example, a simple spray drying process requires consideration of input solution concen-tration and flow rate, airflow rate, and temperature, four factors. If each factor is studied at a high and low level, then this is described as a 2⁴ factorial design.

The advantages of factorial experiments relate to their purpose. The intent is frequently to investigate the effects of each factor over some preassigned range that is covered by the levels of that factor, and not specifically to discover the combination of factors that results in the maximum or minimum response. Where the factors are independent, the statistical analysis is straightforward. However, where the factors are not independent there this additional infor-mation is to be gained through confounding analysis.

Factorial experiments are useful for exploratory experiments where the objective is rapid determination of the effects of a number of factors over a designated range; investigations of interactions among effects of several factors, all combinations of factors give the most information in this regard; experiments designed to lead to recommendations over a broad range of conditions. Where the objective is the latter recommendations, subsidiary factors may be brought into an experiment to test the principal factors under various conditions to those that are encountered in the population to which recommendations are to apply.

Fractional Factorial Design

Often full factorial designs are beyond the resources of the investigator, or the level of precision obtained is substantially higher than required. In a 2⁶ factorial design, each main effect is an average of 32 combinations of other factors. It is possible that it would be sufficient to conduct a four- or eightfold replication and a partial experiment might be considered. Information is lost in this approach to experiments in particular with respect to interactions between factors.

There are hazards associated with this approach. The results of such experiments may be misinterpreted, particularly if the interactions that have been assumed to be negligible are not. The impact of this problem depends on decisions made from the results. In a screening study this may not have a huge impact where the implications for a fundamental research program could be very serious. In general, it is unadvisable to rely heavily on fractional factorial design as a tool for investigation unless the risk of being misled by the occur-rence of factor interactions is considered small.

Central Composite Design

The designs above consider linear (first-order) relationships between levels of particular factors. However, the relationships between levels of factors may be related through nonlinear functions, the simplest of which is a quadratic

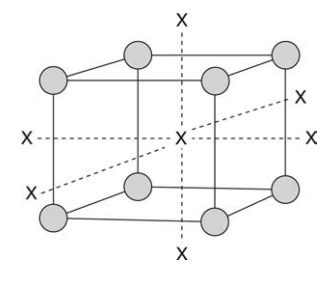
FIGURE 18.1 Central composite design (CCD) based on three factors (x, y, z axes). O, factorial design factor combinations; X, additional orthogo-nal factor combinations to complete the CCD.

response surface (second order) that can emerge from central composite designs (CCDs) based on factorial analysis. CCDs test additional factor combinations. CCD can be fitted into a sequential program of experimentation. The experiment starts with an exploratory 2ⁿ factorial design to which a linear response surface is fitted. If the center of the first experiment is close to a point of maximum response, combinations of factors can be selected orthogonally to one of the original factorial designs to indicate the curvature of the response surface. Figure 18.1 illustrates the way factor combinations would be selected.