Graphical Methods

GRAPHICAL METHODS

A second way to display data is through the use of graphs. Graphs give the reader an overview of the essential features of the data. Generally, visual aids provided by graphs are easier to read than tables, although they do not contain all the detail that can be incorporated in a table.

Graphs are designed to provide visually an intuitive understanding of the data. Effective graphs are simple and clean: thus, it is important that the graph be self-ex-planatory (i.e., have a descriptive title, properly labeled axes, and an indication of the units of measurement).

Using the BMI data, we will illustrate the following seven graphical methods: histograms, frequency polygons, cumulative frequency polygons, stem-and-leaf displays, bar charts, pie charts, and box-and-whisker plots.

1. Frequency Histograms

As we mentioned previously, a frequency histogram is simply a bar graph with the class intervals listed on the x-axis and the frequency of occurrence of the values in the interval on the y-axis. Appropriate labeling is important. For the BMI data described earlier, Figure 3.1 provides an appropriate example of a frequency histogram.

Proper graphing of statistical data is an art, governed by what we would like to communicate. Several excellent books provide helpful guidelines for proper graph-ics. Among the most popular books are two by Edward Tufte [Tufte (1983, 1997)].

TABLE 3.5. Guidelines for Creating Frequency Distributions from Grouped Data

1. Find the range of values—the difference between the highest and lowest values.

2. Decide how many intervals to use (usually choose between 6 and 20 unless the data set is very large). The choice should be based on how much information is in the distribution you wish to display.

3. To determine the width of the interval, divide the range by the number of class intervals selected. Round this result as necessary.

4. Be sure that the class categories do not overlap!

5. Most of the time, use equally spaced intervals, which are simpler than unequally spaced intervals and avoid interpretation problems. In some cases, unequal intervals may be helpful to emphasize certain details. Sometimes wider intervals are needed where the data are sparse.

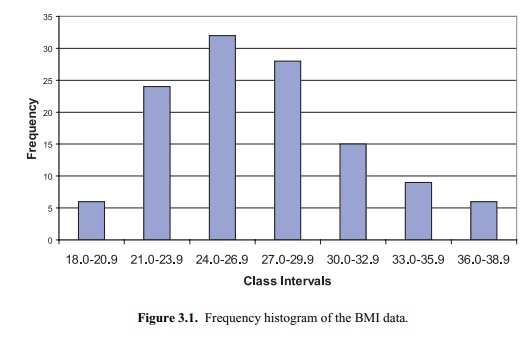
Figure 3.1. Frequency histogram of the BMI data.

Huff’s (1954) popular book illustrates how playing tricks with the scales on a plot can distort information and mislead the reader. These experts provide sage guidance regarding construction of graphs.

Figure 3.2 provides a graph, called a relative frequency histogram, of the same data as in Figure 3.1 with the height of the y-axis represented by the relative frequency (%) rather than the actual frequency. By comparing Figures 3.1 and 3.2, you can see that the shapes of the graphs are similar.

Here the magnitude of the relative frequency is determined strictly by the height of the bar; the width of the bar should be ignored. For equally spaced class intervals, the height of the bar multiplied by the width of the bar (i.e., the area of the bar) also can represent the proportion of the cases in the given class.

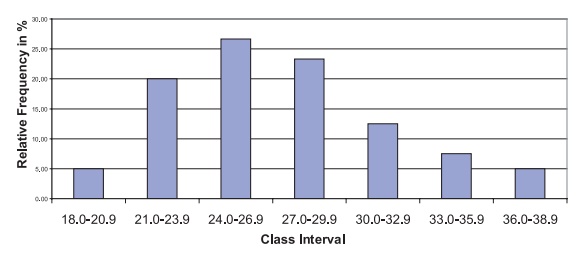
Figure 3.2. Relative frequency histogram for the BMI data.

In Chapter 5, when we discuss probability distributions, we will see that when properly defined, relative frequency histograms are useful in approximating proba-bility distributions. In such cases, the area of the bar represents the percentage of the cases in the interval. When the class intervals have varying lengths, we need to adjust the height of the bar so that the area, not the height, is proportional to the per-centage of cases. For example, if two intervals each contain 10% of the sampled cases but one has a width of 2 units and the other a width of 4 units, we would re-quire that the intervals with width 4 units have one-half of the height of the interval with a width of 2 units.

Figure 3.3 provides a relative frequency histogram for the same BMI data except that we have combined the second and third and fifth and sixth class intervals into one interval; the resulting frequency distribution has five class intervals instead of the original seven.

The first, third, and fifth intervals all have a width of 3 units, whereas the sec-ond and fourth intervals have a width of 6 units. Consequently, the relative per-centages are represented correctly by the height of the histogram but not by the area. The excessive height of the second and fourth intervals is corrected by di-viding the height (i.e., frequency) of these intervals by 2. Figure 3.4 shows the ad-justed histogram.

Figure 3.5 presents a cumulative frequency histogram in which the frequency in the interval is replaced by the cumulative frequency, as we demonstrated in the cu-mulative frequency tables. The analogous figure for cumulative relative frequency (%) is shown in Figure 3.6.

2. Frequency Polygons

Frequency polygons are very similar to frequency histograms. However, instead of placing a bar across the interval, the height of the frequency or relative frequency is plotted at the midpoint of the class interval; these points are then connected by straight lines creating a polygonal shape, hence the name frequency polygon.

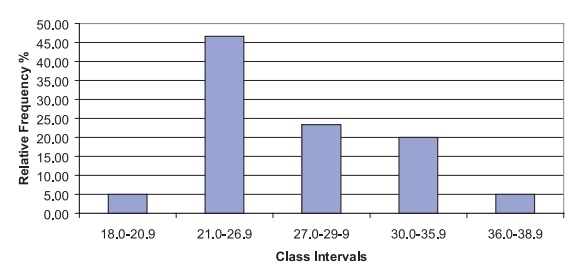
Figure 3.3. BMI data: relative frequency histogram with unequally spaced intervals.

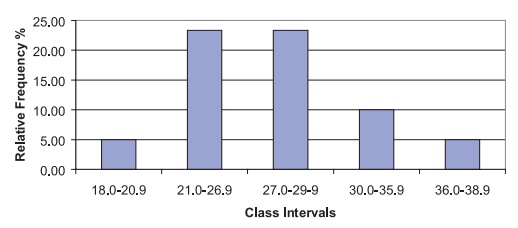
Figure 3.4. BMI data: relative frequency histogram with unequally spaced intervals (height adjusted for correct area).

Figures 3.7 and 3.8 represent, respectively, a frequency polygon and relative fre-quency polygon for the BMI data. These figures are analogous to the histograms presented in Figures 3.1 and 3.2, respectively.

3. Cumulative Frequency Polygon

A cumulative frequency polygon, or ogive, is similar to a cumulative frequency his-togram. The height of the function represents the sum of the frequencies in all the class intervals up to and including the current one. The only differences between a cumulative frequency polygon and a cumulative frequency histogram are that the height is taken at the midpoint of the class interval and the points are connected by straight lines instead of being represented by bars. Figures 3.9 and 3.10 represent, respectively, the cumulative frequency polygon and cumulative relative frequency polygon for the BMI data.

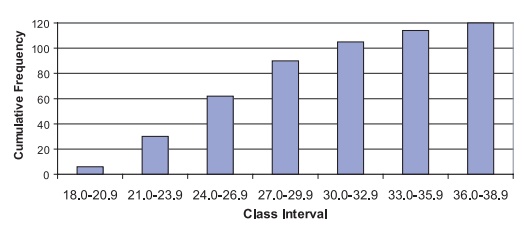
Figure 3.5. Cumulative frequency histogram for BMI data.

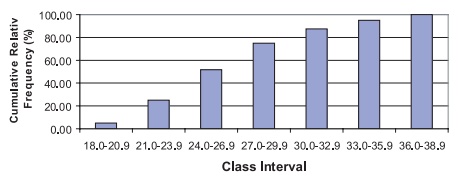
Figure 3.6. Cumulative relative frequency histogram for BMI data.

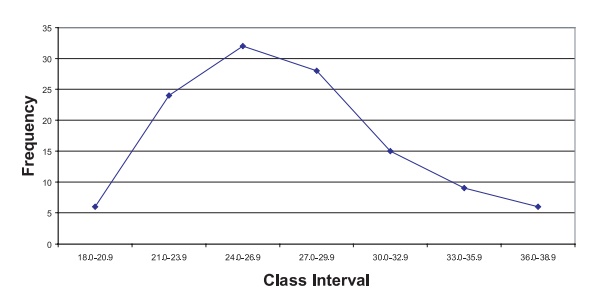
Figure 3.7. Frequency polygon for BMI data.

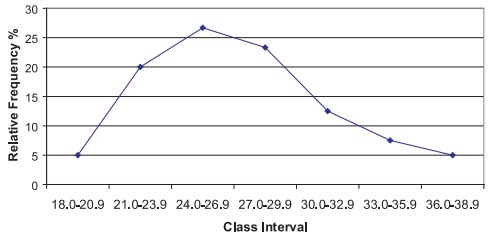
Figure 3.8. Relative frequency polygon for BMI data.

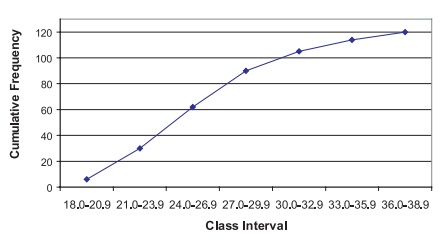
Figure 3.9. Cumulative frequency polygon (ogive) for BMI data.

4. Stem-and-Leaf Diagrams

Histograms summarize a dataset and provide an idea of the shape of the distribution of the data. However, some information is lost in the summary. We are not able to reconstruct the original data from the histogram.

John W. Tukey created an innovation in the 1970s that he termed the “stem-and-leaf diagram.” Tukey (1977) elaborates on this method and other innovative exploratory data analysis techniques. The stem-and-leaf diagram not only provides the desirable features of the histogram, but also gives us a way to reconstruct the entire data set from the diagram. Consequently, we do not lose any information by con-structing the plot.

The basic idea of a stem-and-leaf diagram is to construct “stems” that represent the class intervals and to have “leaves” that exhibit all the individual values. Let us demonstrate the technique with the BMI data. Recall that these data ranged from a lowest value of 18.3 to a highest value of 38.8. The class groups will be the integer part of each number; any value from 18.0 to 18.9 will belong to the first stem, from 19.0 to 19.9 to the second stem, and continuing to the highest value in the dataset.

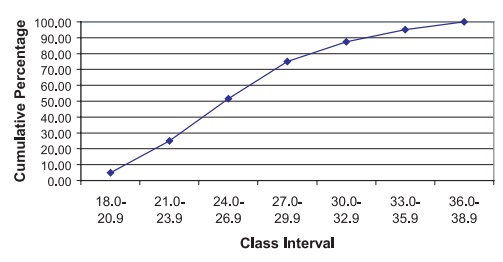
Figure 3.10. Cumulative relative frequency polygon for BMI data.

To form the leaves, we place a single digit for each observation that belongs to that class interval (stem). The value used will be the single digit that appears after the decimal point. If a particular value is repeated in the data set, we repeat that val-ue on the leaf as many times as it appears in the data set. Usually the numbers on the leaf are placed in increasing order. In this way, we can exhibit all of the data. Inter-vals that include more observations than others will have longer leaves and thus produce the frequency appearance of a histogram. The display of the BMI data is:

18. 3

19. 28

20. 278

21. 111335999

22. 333457789

23. 011345

24. 000112335667788

25. 04446778899

26. 255569

27. 1333344444556

28. 233346778889

29. 358

30. 01238899

31. 01366

32. 68

33. 62

34. 289

35. 0589

36. 6

37. 158

38. 28

From this display, we are able to reach several conclusions about the frequency of cases in each interval and the shape of the distribution, and even reconstruct the original dataset, if necessary. First, it is apparent that the intervals that contain the highest and second-highest frequencies of observations are 24.0 to 24.9 and 25.0 to 25.9, respectively. Also, empty or low-frequency intervals such as 36.0 to 36.9 are recognized easily. Second, the shape of the distribution is also easy to visualize; it resembles a histogram placed sideways. The individual digits on the leaves repre-sent all of the 120 observations.

The frequencies associated with each of the class intervals are calculated by to-taling the number of digits on the corresponding leaf. Each individual value can be reconstructed by observing its stem and leaf value. For example, the 9 in the fourth row of the diagram represents the value “21.9” because 21 is the stem for that row and 9 is the leaf value. The stem represents the digits to the left of the decimal place and the leaf the digit to the right.

Table 3.5 reconstructs the stem-and-leaf diagram shown in the foregoing dis-play. In addition, the table illustrates the class interval associated with the stem and provides the frequency counts obtained from the leaves.

5. Box-and-Whisker Plots

John W. Tukey created another scheme for data analysis, the box-and-whisker plot. The box-and-whisker plot provides a convenient and compact picture of the general shape of a data distribution. Although it contains less information than a histogram, the Box-and-Whisker plot can be very useful in comparing one distribution to other distributions. Figure 3.11 presents a box-and-whisker plot in which the distribution of weights is compared for patients diagnosed with cancer, diabetes, and coronary heart disease. From the figure, we can see that although the distributions overlap, the average weight increases for each of these diagnoses.

To define a box-and-whisker plot, we must give definitions of several terms related to the distribution of a data set; these terms are the median, a-percentile, and the interquartile range. 

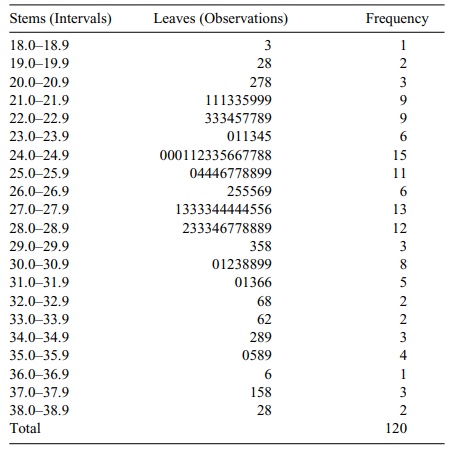
TABLE 3.5. Stem-and-Leaf Display for BMI Data

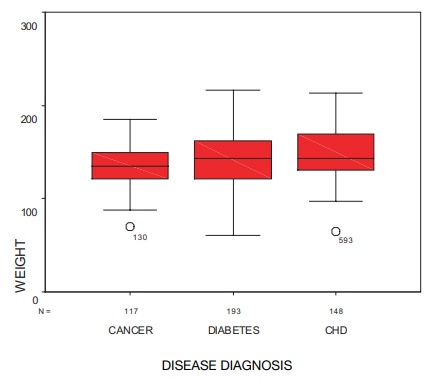
Figure 3.11. Box-and-whisker plot for female patients who have cancer, diabetes, and coronary heart disease (CHD). (Source: Robert Friis, unpublished data.)

The median of a data set is the value of the observation that divides the ordered dataset in half. Essentially, the median is the observation whose value defines the midpoint of a distribution; i.e., half of the data fall above the me-dian and half below.

A precise mathematical definition of a median is as follows: If the sample size n is odd, then n = 2m + 1, where m is an integer greater than or equal to zero. The me-dian then is taken to be the value of the m + 1 observation ordered from smallest to largest. If the sample size n is even, then n = 2m where m is an integer greater than or equal to 1. Any value between the mth and m + 1st values ordered from smallest to largest could be the median, as there would be m observed values below it and m observed values above it. When n is even, a convention that makes the median unique is to take the average of the mth and m + 1st observations (i.e., the sum of the two values divided by 2).

The α-percentile is defined as the value such that a percent of the observations have values lower than the α -percentile value; 100 – α percent of the observations are above the a-percentile value. The quantity α is a number between 0 and 100. The median is a special case in which the α = 50.

We use specific a-percentiles for box-and-whisker plots. We can draw these plots either horizontally, or vertically as in the case of Figure 3.11. The a-per-centiles of interest are for α = 1, 5, 10, 25, 50, 75, 90, 95, and 99. A box-and-whisker plot, based on these percentiles, is represented by a box with lines (called whiskers) extending out of the box in both north and south directions. These lines terminate with bars perpendicular to them. The lower end of the box represents the location of the 25th percentile of the distribution. Inside the box, a line is drawn to mark the location of the median, or 50th percentile, of the distribution. The upper end of the box represents the location of the 75th percentile of the distribution.

The length of the box is called the interquartile range, the range of values that constitute the middle half of the data. Out of the upper and lower ends of the box are the lines extending to the perpendicular bars called whiskers, which represent ex-tremes of the distribution.

While there are no consistent standards for defining the extremes, people who construct the plots need to be very specific about the meaning of these extremes. Often, these extremes correspond to the smallest and largest observations, in which case the length from the end of the whisker on the bottom to the end of the whisker on the top is the range of the data.

In many applications, the ends of the whiskers represent a-percentiles. For ex-ample, choices can be 1 for the end of the lower whisker and 99 for the end of the upper whisker, or 5 for the lower whisker and 95 for the upper whisker. The forego-ing are the most common choices; however, sometimes 10 and 90 are used for the lower and upper whiskers, respectively.

Sometimes, we consider the minimum (i.e., the smallest value in the data set) and the maximum (i.e., the largest value in the data set) to be the ends of whiskers. In this text, we will assume that the endpoints of the whiskers are the minimum and maximum values of the data. If other percentiles are used, we will be careful to state their values.

The box plot is very useful for indicating the presence or absence of symmetry and for comparing spread or variability of two or more data sets. If the distribution is not symmetric, it is possible that the median will not be in the center of the box and that the whiskers will not be the same length. Looking at box plots is a very good first step to take when analyzing data.

If a box-and-whisker plot indicates the presence of symmetry, the distribution may be a normal distribution. Symmetry means that if we split the distribution (i.e., probability density function) at the median, the half to the right will be the mirror image of the half to the left. For a box-and-whisker plot that shows a symmetric dis-tribution: (1) the median will be in the middle of the box; and (2) the right and left whiskers will have equal lengths. Regardless of the definition we choose for the ends of the whiskers, points one and two will be true.

Concluding this section, we note that Chapters 5 and 6, respectively, describe probability distributions and the normal distribution. The normal, or Gaussian, dis-tribution is a symmetric distribution used for many applications. When the data come from a normal distribution, the sample should appear to be nearly symmetric. So for normally distributed data, we expect the box-and-whisker plot to have a me-dian near the center of the box and whiskers of nearly equal width. Large deviations from the model of symmetry suggest that the data do not come from a normal distri-bution.

6. Bar Graphs and Pie Charts

Bar graphs and pie charts are useful tools for summarizing categorical data. A bar graph has the same form as a histogram. However, in a histogram the values on the x-axis represent intervals of numerically ordered data. Consequently, as we move from left to right on the x-axis, the intervals represent increasing values of the vari-able under study. As categorical data do not exhibit ordering, the ordering of the bars is arbitrary. Meaning is assigned only to the height of the bar, which represents the frequency or relative frequency of occurrence of cases that belong to that partic-ular class interval. In addition, the width of the bar has no meaning.

Pie charts depict the same information as do bar graphs, but in the shape of a circle or pie. The circle is divided into wedges, one for each category of the data. The size of each wedge is determined by its angular measurement. Since a circle contains 360°, a wedge that contains 50% of the cases would have an angular measurement of 180°. In general, if the wedge is to contain a percent of the cases, then the angle for the wedge will be 360a/100°. Figure 3.12 illustrates a pie chart of categorical data. Using data from a research study of clinic patients, the figure presents the proportions of female patients who were diagnosed with cancer, diabetes, and coronary heart disease.

We can use pie charts also to represent ordinal data. Table 3.6 presents data regarding a characteristic called the Pugh level, a measure of the severity of liver dis-ease. Figure 3.13 illustrates these data in the form of a pie chart. Based on 24 pediatric patients with liver disease, this pie chart presents ordinal data, which indicate severity of the disease. As an alternative to a pie chart, Figure 3.14 shows a bar graph for the same Pugh data presented in Table 3.6.

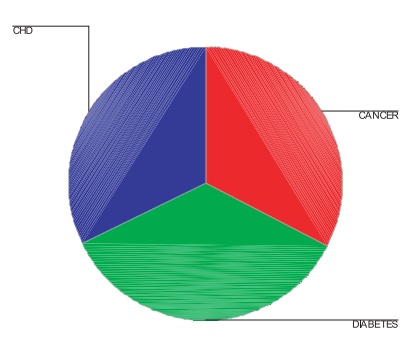
Figure 3.12. Pie chart—proportions of patients diagnosed with cancer, diabetes, and coronary heart dis-ease (CHD). (Source: Robert Friis, unpublished data.)

TABLE 3.6. Pugh Categories and Pugh Severity Levels

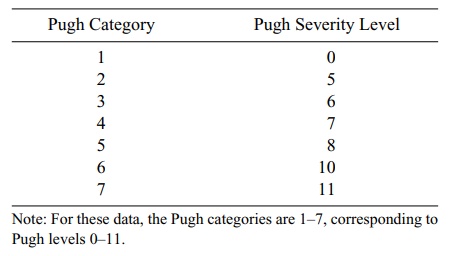
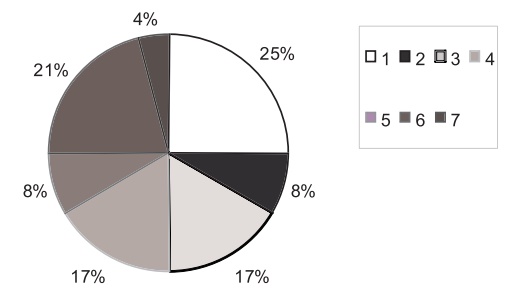
Figure 3.13. Pie chart for Pugh level for 24 children with liver disease.

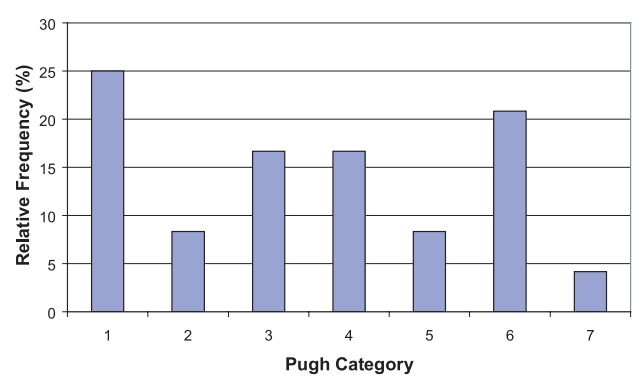
Figure 3.14. Relative frequency bar graph for Pugh categories of 24 pediatric patients with liver dis-ease.