Exercises questions answers
| Home | | Advanced Mathematics |Chapter: Biostatistics for the Health Sciences: Systematic Organization and Display of Data
Biostatistics for the Health Sciences: Systematic Organization and Display of Data - Exercises questions answers
EXERCISES
3.1 Define the term “variable” and describe the
following types of variables:
a. Qualitative
(1) Nominal
(2) Ordinal
b. Quantitative
(1) Interval
(2) Ratio
c. Discrete versus continuous
3.2 The following terms relate to frequency tables.
Define each term.
a. Class interval
b. Class frequency
c. Relative frequency percentage
d. Cumulative frequency
e. Cumulative relative frequency
f. Cumulative percentage
3.3 Define the following graphical methods and
describe how they are used.
a. Histogram
b. Relative frequency histogram
c. Frequency polygon
d. Cumulative frequency polygon (ogive)
3.4 How does one construct a stem-and-leaf diagram?
What are the advantages of this type of diagram?
3.5 How may the box-and-whisker plot be used to
describe data? How are the fol-lowing terms used in a box-and-whisker plot?
a. Median
b. Alpha percentile
c. Interquartile range
3.6 Refer to the following dataset that shows the
class interval (and frequency in parentheses):
{0.0–0.4 (20); 0.5–0.9 (30); 1.0–1.4 (50); 1.5–1.9
(40); 2.0–2.4 (10); 2.5–2.9 (20); 3.0–3.4 (20); 3.5–3.9 (10)}
Construct a relative frequency histogram, a
cumulative frequency histogram, a relative frequency (%) histogram, a
cumulative relative frequency (%) his-togram, a frequency polygon, and a
relative frequency polygon. Describe the shapes of these graphs. What are the
midpoint and limits of the interval, 2.0–2.4?
3.7 Using the data in Table 3.7, construct a frequency
table with nine intervals and then calculate the mean and median blood levels.
TABLE 3.7. Blood Levels (mg/dl) of 50 Subjects
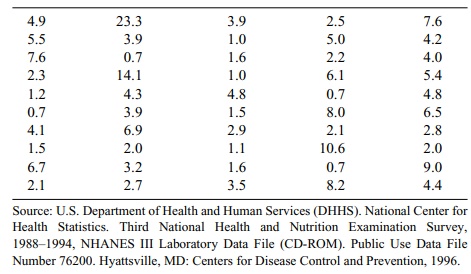
3.8 Take the data set from Exercise 3.7 and order the
observations from smallest to largest. Determine the lower and the upper
quartiles and generate a box-and-whiskers plot for the data using the smallest
and largest observations for the whiskers.
3.9 Take the data from Exercise 3.7 and construct a
stem-and-leaf plot using the integer part of the number for the stem and the
digit to the right of the decimal point for the leaf.
3.10 Consider the following data set: {3, 4, 8, 5, 7, 2,
5, 6, 5, 9, 7, 8, 6, 4, 5}. De-termine the median and quartiles, and the
minimum and maximum values.
3.11 Using the data presented in Table 3.8, calculate
the mean, median, and quar-tiles, and construct a box-and-whisker plot.
TABLE 3.8. Ages of Patients in a Primary Care Medical Clinic (n = 50)
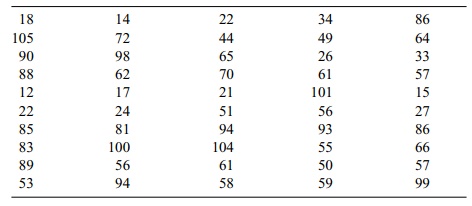
3.12 Construct a frequency histogram and a cumulative
frequency histogram with the data
from Exercise 3.11 using the following class intervals: 10–19, 20–29, 30–39,
40–49, 50–59, 60–69, 70–79, 80–89, 90–99, 100–109.
3.13 Construct a stem-and-leaf plot with the data from
Exercise 3.11.
3.14 Classify the following data as either (1) nominal,
(2) ordinal, (3) interval, or (4) ratio.
a. The names of the patients in a clinical trial
b. A person’s weight
c. A person’s age in years
d. A person’s blood type
e. Your top ten list of professional basketball players ranked in ascending
order of preference
f. The face of a coin that lands up (a head or a tail)
3.15 The following questions (a-d) refer to the data
presented in Table 3.9.
a. Construct a frequency table with the class intervals 0–1, 2–3, 4–5, 6–7,
8–9, 10–11, and 12–13.
b. Construct a frequency histogram of the weight losses.
c. Construct a frequency polygon and describe the shape of the
distribution.
d. What is the most common weight loss?
3.16 The FBI gathers data on violent crimes. For 20,000
murders committed over the past few
years, the following fictitious data set represents the classifica-tion of the
weapon used to commit the crime.
12,500 committed with guns
2,000 with a knife
5000 with hands
500 with explosives
Construct a pie chart to describe this data.
3.17 In 1961, Roger Maris broke Babe Ruth’s home run
record by hitting 61 home runs.
Ruth’s record was 60. The following set of numbers is the consecutive list of
home run totals that Ruth collected over a span of 15 seasons as a Yan-
TABLE 3.9. Weight Loss in Pounds of Individuals on a Five-Week Weight
Control Program (n = 25)

kee: 54, 59, 35, 41, 46, 25, 47, 60, 54, 46, 49, 46,
41, 34, 22. Maris had a 10-year career in the American League before joining
the St. Louis Cardinals in the National League at the end of his career. Here
is the list of home runs Maris hit during his 10 years: 14, 28, 16, 39, 61, 33,
23, 26, 8, 13
a. Find the seasonal median
number of home runs for each player.
b. For each player, determine the
minimum, the first quartile, the median, the third quartile, and the maximum of
their home run totals. Use these results to construct comparative
box-and-whisker plots. These five numbers that highlight a box plot are called
the five-number summary.
c. How do the two distributions
differ based on the box plots?
3.18 In 1998, Mark McGwire broke Roger Maris’ home run
record of 61 by hitting 70 home
runs. Incredibly, in the same year Sammy Sosa also broke the record, hitting
66. Again, in 1999 both players broke Maris’ mark but did not top their 1998
results: McGwire hit 65 and Sosa 63. In 2001, another slugger, Barry Bonds,
whose top home run total was 49 in 2000, broke McGwire’s record with 73 home
runs. Here we present the seasonal home run totals for McGwire over his major
league career starting with his rookie 1987 season, along with those for Sammy
Sosa, Barry Bonds and Ken Griffey Jr.
McGwire 49, 32, 33, 39, 22, 42, 9, 9, 39, 52, 58, 70,
65, 32
Sosa 4, 15, 10, 8, 33, 25, 36, 40, 36, 66, 63, 50
Bonds 16, 25, 24, 19, 33, 25, 34, 46, 37, 33, 42,
40, 37, 34, 49
Griffey 16, 22, 22, 27, 45, 40, 17, 49, 56, 56, 48,
40
McGwire’s low totals of 9 in 1993 and 1994 are
explained by a combina-tion of the baseball strike that cancelled many games
and some injuries he sustained. Sosa’s rookie year was 1989. His home run
totals were fairly high during the strike years. Bonds’ rookie year was 1986.
He has been a consis-tent home run hitter but has never before approached the
total of 60 home runs.
Ken Griffey Jr. had a spectacular start during the
strike season, and many thought he would have topped Maris that year had there
not been a strike. Griffey’s rookie year was 1989. In the strike-shortened
season of 1993, Grif-fey hit 45 home runs; he has approached 60 twice.
a. Find the seasonal median
number of home runs for each player.
b. For each player, determine the
minimum, the first quartile, the median, the third quartile, and the maximum of
their home run totals. Use these results to construct comparative
box-and-whisker plots.
c. What are the similarities and
differences among these famous sluggers?
3.19 In 2001, due to injury, McGwire hit only 29 home
runs; Sosa hit 64 home runs; Bonds
hit 73 home runs for a new major league record; and Griffey hit 22. Their
current career home runs are as follows:
McGwire 49, 32, 33, 39, 22, 42, 9, 9, 39, 52, 58,
70, 65, 32, 29
Sosa 4, 15, 10, 8, 33, 25, 36, 40, 36, 66, 63, 50, 64
Bonds 16, 25, 24, 19, 33, 25, 34, 46, 37, 33, 42,
40, 37, 34, 49, 73
Griffey 16, 22, 22, 27, 45, 40, 17, 49, 56, 56, 48,
40, 22
a. Find the seasonal median number of home runs for each player.
b. For each player, determine the minimum, the first quartile, the median,
the third quartile and the maximum of their home run totals. Use these results
to construct comparative box-and-whisker plots.
c. What are the similarities and differences among these famous sluggers?
d. Did the results from 2001 change your conclusions from the previous
problem? If so, how did they change and why?
Answer:
3.7 Since the range is from 0.7 to 23.3 and we are to
choose 9 intervals, we choose to
divide the data into 9 equal width intervals from 0 to 24.3, each of length
2.7. Data points at an interval boundary are included in the higher of the two
intervals.
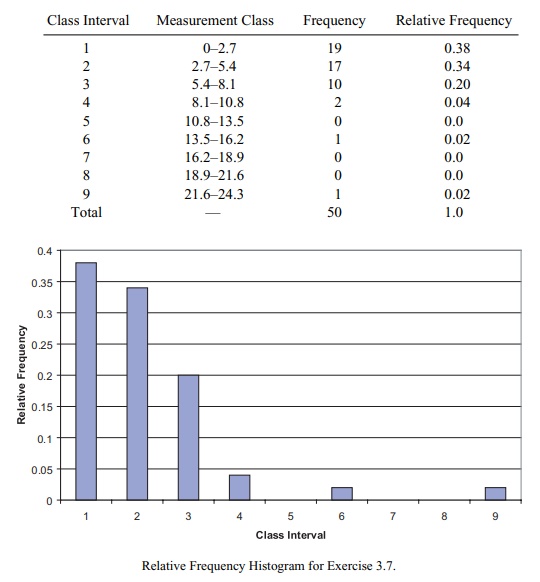
Relative Frequency Histogram for Exercise 3.7.
The mean is 4.426 and the median is 3.90.
3.9
The numbers range from 0.7 to
23.3, so the stem and leaf plot looks as follows:
0. 7777
1. 00125566
2. 0011235789
3. 25999
4. 01234889
5. 045
6. 1579
7. 66
8. 02
9. 0
10.
6
11.
12.
13.
14.
1
15.
16.
17.
18.
19.
20.
21.
22.
23.
3
3.10 The median is 5. The lower quartile is 4 and the
upper quartile is 7. The smallest
value is 2 and the largest 9.
Related Topics
