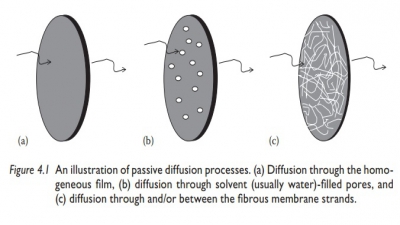
Principles of diffusion
| Home | | Pharmaceutical Drugs and Dosage | | Pharmaceutical Industrial Management |Chapter: Pharmaceutical Drugs and Dosage: Biopharmaceutical considerations
Passive diffusion leads to change in concentration in a region over a period of time and space.
Principles of
diffusion
Passive
diffusion leads to change in concentration in a region over a period of time
and space. Fick’s laws of diffusion quantitate the amount of solute diffusing
per unit time and area as a function of concentration gradient of solute in the
direction of diffusion. These laws also relate the changes in solute
concentration in a given region over time to the change in concentra-tion
gradient of the solute in that region.
Fick’s first law
Fick’s
law of diffusion postulates that the diffusing molecules go from regions of
high concentration to regions of low concentration. The rate of diffusion, the
amount of material (M) flowing
through a unit cross-section (S) of a
barrier in unit time (t) is defined
as the flux (J). Flux is related to
the concentration gradient (dC = C1−C2) between the donor region at a higher concentration (C1) and the receiving region
at a lower concentration (C2)
per unit distance (x) by the
following expression:

where:
J is the flux, in
g/(cm2s)
S is the
cross-section of the barrier, in cm2
dM /dt
= rate of diffusion,
in g/s (M = mass in g; t = time in s)
The
flux is proportional to the concentration gradient, dC/dx:

where:
D is the diffusion
coefficient of a penetrant, in cm2/s
C is the concentration,
in g/cm3 or g/mL
x is the distance
perpendicular to the surface of the barrier, in cm
Thus,
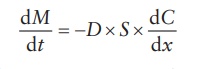
The
negative sign in this equation signifies that diffusion occurs in a direc-tion
of decreasing concentration. Thus, the flux is always a positive quantity.
Although the diffusion coefficient, D,
or diffusivity, as it is often called, appears to be a proportionality
constant, it does not remain constant. It is affected by changes in
concentration, temperature, pressure, solvent proper-ties, molecular weight,
and chemical nature of the diffusant. For example, the larger the molecular
weight, the lower the diffusion coefficient.
Fick’s second law
Fick’s
second law predicts changes in solute concentration over time caused by diffusion.
It states that the change in concentration with time in a par-ticular region is
proportional to the change in the concentration gradient at that region in the
system. Concentration of solute or diffusant, C, in the volume of the region, x,
changes as a result of the net flow of diffusing molecules in or out of the
region. This change in concentration with time, t (i.e., dC/dt), is proportional to the change in the
flux of diffusing mol-ecules, J, per
unit distance, x (i.e., dJ/dx).

Differentiating
the equation of flux, J, as per
Fick’s first law of diffusion ( J = −D × d C /dx), with respect to x, we obtain:
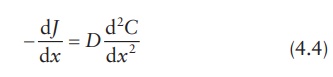
Therefore,
concentration and flux are often written as C(x, t)
and J(x, t), respectively, to
emphasize that these parameters are functions of both dis-tance, x, and time, t. Substituting dC/dt for −dJdx, Ficks’s second law of diffusion can
be expressed as:
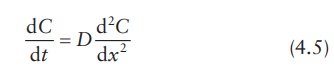
This
equation represents diffusion only in one direction. To express con-centration
changes of diffusant in three dimensions, Fick’s second law of diffusion is
written as:
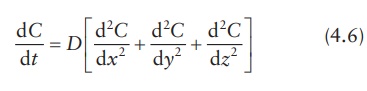
Related Topics